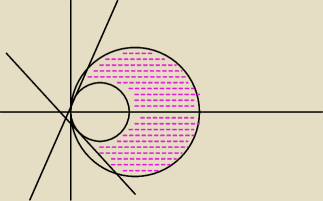
Obliczanie całki podwójnej, koło, przedziały dla fi magicznyukf: ∬√x² + y² D= 2x<x²+y²<4x −x<y<√3 Przekształciłem pierwszy wzór, wyszły z tego dwa inne: 1<(x−1)² + y² oraz (x−2)²+y²<4 Wyznaczyłem r, które wynosi: 2cos(fi)<r<4cos(fi) i teraz nie wiem jak wyznaczyć przedziały dla fi. Pomożecie? Sytuacja jest mniej więcej taka jak na rysunku.

'Leszek: Obszar D jakos nie tak powinien wygladac ,zwlaszcza czesc druga , czy to jest taka nierownosc, −x < y < √3 ?, czegos chyba brakuje ?

magicznyukf: aa przepraszam, brakuje x −x < y < √3x

'Leszek: To wobec tego −π/4 ≤ φ ≤ π/3

magicznyukf: Mógłbyś wyjaśnić skąd to się wzięło?

'Leszek: Takie sa linie y = −x oraz y = √3 x , te linie tworza odpowiednie katy z osia X .