. Piotrek: Wyznacz równanie elipsy E, wiedząc że punkt F jest jednym z jej ognisk i punkt A ∊ E , gdy F= ( 0 , 12 ) , A = ( −5 , 0 ).

	(x−x0)2		(x−y0)2
Mam równanie elipsy		+		= 1
	a2		b2

Jak to ruszyć ?

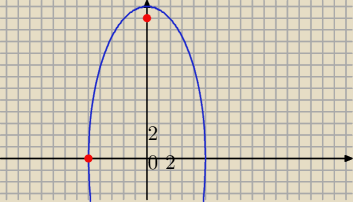
'Leszek: Ognisko F( 0 , 12 ) ⇒ c = 12 , oraz c² = b² − a² oraz A(−5,0) ⇒ a = 5 Czyli b = 13 , x_o = 0 ,y{o} = 0 , wykonaj rysunek , elipsa jest " wydluzona na osi Y "

Mila:

Piotrek: Cześć Mila Pan P.... 10 pozdrawia

Mila: Witaj, jak Ci się wiedzie?

Piotrek: Aby do przodu , zaraz koniec I roku studiów i konczę przygodę z matematyką już, bo na tych studiach już nie bede miał matematyki. W przyszłym tyg egzamin , aby zdać

Piotrek: Muszę nadrabiać materiał, bo nie było prowadzącego i nie miałem matematyki w ogóle

Piotrek: W 1 semestrze, miałem z egz. 4.5 i 5 z ćwiczeń, więc mimo przerwy w nauce , coś z myślenia pozostało

Mila: To do pracy, aby sukces był, czego Ci życzę Jak ten czas leci.

Mila: Piękne wyniki w I semestrze. Gratulacje.

Piotrek: Dziękuję! Wrócę jeszcze do tematu wg książki mam, że a − półoś wielka elipsy, a b − półoś małay elipsy więc chyba b= 5 i a = 13 powinno być bo gdyby były x_o i y₀ nie równały się zero to miało by to znaczenie Więc jak to powinno być ?

'Leszek: Oznaczenia w matematyce nie maja zasadniczego znaczenia : np : ax² + bx + c = 0 , Δ = b² − 4ac mx² + px − q = 0 , Δ = p² − 4mq , i.t.d nie ucz sie matematyki na pamiec wzorow , zas ucz sie pojeciowo , powodzenia ! !

Piotrek: to wiem, ale jeśli w mianowniku jest y₀ i podziele sobie obojętnie przez jakąś półoś to będzie coś nie tak...

Piotrek: w liczniku y_o lub x₀

'Leszek:

	x2		y2
Rownanie tej elipsy :		+		= 1 , podstaw A (−5,0)
	52		132

i sprawdz , ze sie szystko sie zgadza ! Pani Mila pokazala Ci prawidlowy rysunek , proponowalem Ci zebys go zrobil dla sprawdzenia ,w matematyce a zwlaszcza w geometrii rysunki sa jak najbardziej przydatne , rozwijaja spostrzegawczosc i pamiec wzrokowa ! !

Piotrek: ok

Piotrek: Szeregi ///

	√n
∑
	n2+n + 1

Wykazuje zbieżność

√n		√n		1
	≤		=
n2+n + 1		n2		n3/2

1
	− szereg Dirchleta zbieżny
n3/2

	√n
wiec na mocy k. porównawczego ∑		jest zbieżny
	n2+n + 1

może być taka nierówność ?

Piotrek: Porobiłem z elipsą, jak możesz to sprawdź wyniki b) F= (−12,0 ), A ( 0, 5)

x2		y2
	+		= 1
132		252

c) F(24,0) , A(0,−7)

x2		y2
	+		= 1
252		72

d) F= ( 0 , − 24) A= ( 7,0)

x2		y2
	+		= 1
72		252

'Leszek:

	x2		y2
W przypadku b) masz blad w druku ,powinno byc :		+		= 1
	132		52

Pzostale przyklady sa dobrze zrobione !

Piotrek: ok, dziękuję

Adamm: może być taka nierówność

jc: To nie jest ogólne równanie. Stawiamy w dowolnym miejscu F₂, uważając aby A nie leżało na odcinku F₁F₂, a potem rysujemy: |P−F₁| + |P−F₂| = |A−F₁| + |A−F₂|.

Piotrek: ok, jeszcze bede mial potem 2 zadania z elipsy i hiperboli. Może i to proste jest, ale nie miałem tego w ogóle na ćwiczeniach