Sprawdź czy f jest suriekcją Jimmy: Witam, mam problem z zadaniem, niestety kompletnie nie wiem jak się zabrać głównie do drugiej jego części rozpoczynającej się od wskaż: f:R−>R , f(x)=(x+1)²−2. Rozstrzygnij czy f jest suriekcją. Wskaż f(A) oraz f⁻¹(A) dla A=(2,7>

Jimmy: Swoją drogą wyszło mi, że nie jest, ponieważ dla y=−3 nie ma takiego x, żeby osiągnąć go tym wzorem. Dobrze? Drugiej części niestety nie potrafie nawet zacząć.

jc: Szukany zbiór to zbiór rozwiązań nierówności 2 < f(x) ≤ 7.

Jimmy: Dobra teraz pewnie głupie pytanie jaka jest różnica pomiędzy f(A) a f⁻¹(A)? I coś dalej jeszcze trzeba z tym zrobić? Gdyby ktoś był w stanie mi rozpisać to zadanie krok po kroku to byłbym wdzięczny

Adamm: f(A) to zbiór wszystkich f(x) takich że x należy do A f⁻¹(A) to zbiór wszystkich x takich że f(x) należy do A

Adamm: f(x)=(x+1)²−2 f(x) jest rosnąca dla wartości z A, oraz ciągła f(2)=7, f(7)=62 zatem f(A)=(7;62> dla f⁻¹(A) wystarczy rozwiązać nierówność podaną przez jc

Jimmy: jeszcze raz potrzebowałbym pomocy tym razem z tym przykładem: Niech f:R−> <2,nieskoń) będzie funkcją określoną wzorem f(x)=max{2,|x|}. Sprawdź czy funkcja jest suriekcją oraz wskaż f(A), f⁻¹(B) gdy A=<−3,0) , B={2,4}. Kompletnie nie rozumiem jak rozwiązać tego maxa po prostu nie daje rady. Czy ktoś mógłby mi z tym pomóc? Orientuję się tylko w tym, że mam wybrać większą wartość po obliczeniu |x| tylko co dalej?

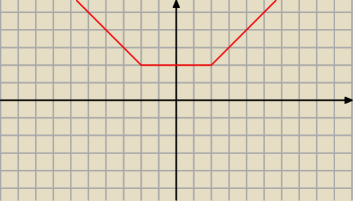
Adamm: max{2, |x|} = 2 dla 2≥|x| |x| dla |x|≥2 funkcja jest suriekcją f(A)=<2;3> f⁻¹(B)=<−2;2>∪{−4;4}