Pomoże kto?
po prostu Michał: Objętość bryły ograniczona powierzchniami
y=x2,y=1, z=0, z=x2+y2
7 cze 17:34
po prostu Michał:
chociaż wskazówka? : /
7 cze 17:48
Adamm: ∫−11∫x21∫0x2+y2dzdy
7 cze 17:48
Adamm: dzdydx
7 cze 17:48
po prostu Michał: jak to panie Adamie , jak?
7 cze 17:49
Adamm: co znaczy "jak"?
7 cze 17:53
Adamm: no więc tak
spróbuj wyznaczyć granice, ale może samemu
nie patrz na to co napisałem
7 cze 17:59
Jack: No wiec probowalem ale mam slaba wyobraznie i tego nie widze

7 cze 18:03
Adamm: Jack, czy ty jesteś Michał ?
7 cze 18:04
Adamm: może tak
czym jest z=x2+y2 ?
wiesz jak wygląda ta powierzchnia ?
7 cze 18:06
po prostu Michał: dobre pytanie − Jack − co probowales?
Adamm − oczywiscie jest to okrag ?
7 cze 18:07
Adamm: nie, jest to paraboloida
taka rodzina okręgów zawieszonych na różnych wysokościach
w każdym razie wygląda ona z boku jak parabola, i jest z całą pewnością ponad
płaszczyzną z=0
7 cze 18:09
Adamm: zatem ograniczenia na z już mamy, 0≤z≤x2+y2
teraz spróbuj ograniczenia na y
7 cze 18:10
po prostu Michał:
nie wiem jak narysowac parabole y=x
2 w 3D
7 cze 18:11
Adamm: paraboloida obrotowa dla ścisłości
7 cze 18:12
po prostu Michał: kojarze wyglad paraboloidy... a nie wiedzialem ze to to , hmm
7 cze 18:12
po prostu Michał:
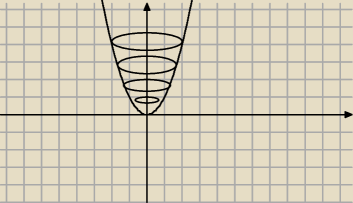
7 cze 18:14
po prostu Michał: ehh, i wez tu cos wyznacz skoro narysowac nie potrafisz ; /
7 cze 18:16
Adamm: y=x2 to jest parabola, tylko z jest dowolne
więc to będzie taka rodzina paraboli, każda różniąca się o to na jakiej wysokości jest
zawieszona
7 cze 18:16
po prostu Michał: tego akurat nie potrafie narysowac.
7 cze 18:17
Adamm: no łatwiej to by było sobie narysować, bo lepsze to niż opis słowny
jak nie masz dobrej wyobraźni to niestety trudno sobie z tym poradzić
7 cze 18:17
7 cze 18:18
po prostu Michał: wyglada jak siodlo ; D
7 cze 18:20
po prostu Michał: albo jednak nie... xd
7 cze 18:21
Adamm: z jakiegoś powodu wolfram to źle narysował
najlepiej wejdź w jakiś inny program, np. geogebra
7 cze 18:23
7 cze 18:26
po prostu Michał: wyglada tak samo jak w wolframie
7 cze 18:26
Adamm: tam masz z=y
2 
7 cze 18:27
Adamm: chodziło o to że osie są źle zaznaczone, ale w sumie nieważne
7 cze 18:27
po prostu Michał: nie widze nigdzie inaczej

7 cze 18:35
Jack: Nie chxe sie wtracac, ale czy czasem plaszcztzna z=0 i paraboloida z = x2 + y2 to nie maja
czesci wspolnej?
8 cze 08:12
jc:
Objętość = ∫−11 dx ∫x2 1 (x2+y2) dy = ... = 88/105
8 cze 09:07
po prostu Michał: hmm
8 cze 22:19

 nie wiem jak narysowac parabole y=x2 w 3D
nie wiem jak narysowac parabole y=x2 w 3D


