Trygonometria zadania Jan: Witam potrzebuje pomocy z trzema zadaniami z trygonometrii których nie umiem zrobić a koniecznie muszę je mieć na jutro. Za wszelkie wskazówki z góry dziękuję Zad1. Oblicz tgα jeśli: sinα − cosα = ^√2₂ i x∊(^π₄; ^π₂)

Jan: Tworząc układ równań z jedynką trygo wychodzi mi sin = ¹_4cosα Co z tym dalej robić?

'Leszek: Podnies obie strony do kwadratu i otrzymasz : sin 2α = 1/2 ⇒ 2α = π/6 + 2kπ ⇒ ⇒α = π/12 + π k , lub 2α = 5π/6 + 2kπ , czyli α = 5π/12 , oblicz tg α = .......

Adamm: podnosząc do kwadratu mamy

	1
sinxcosx=
	4

cosx≠0 ponieważ x∊(π/4; π/2)

	1
tgx=
	4cos2x

	1
zauważmy że		=tg2x+1
	cos2x

0=tg²x−4tgx+1 Δ=12

	4±2√3
tgx=
	2

no ale że x∊(π/4; π/2) to tgx>tg(π/4)=1 więc tgx=2+√3

Jan: Gdy liczyłem w ten sposób wyszły mi faktycznie te x'y x1 = π/12 + kπ x2 = 5/12π + kπ. Tylko jak ja mam to uwzględnić w przedziale α∊(π/4; π/2) ? W sensie że jedno rozwiązanie aby zostanie? Co potem z tym zrobić?

Jan: Adamm skąd tgα = 1/(4cos² x) ?

Adamm: podziel przez cos²x

Jan: A dalszy fragment? Skąd 1/(cos²x) = tg²x+1 ?

Jan: hmmm?

Adamm:

	sin2x		sin2x+cos2x		1
tg2x+1=		+1=		=
	cos2x		cos2x		cos2x

Jan: Wielkie dzięki Mam jeszcze 2 te zadanka. Z tym próbowałem walczyć, jakby ktoś mógł rzucić okiem Zad2. Dla jakich wartości parametru a równanie cos² x = ^{a2 − 3a +2} _a+1 ma rozwiązania? Jako iż zbiorem wartości cos² x będzie przedział <0;1> to zapisałem założenia : ^{a2 − 3a +2} _a+1 ≥0 i ^{a2 − 3a +2} _a+1 ≤1 no i a+1 ≠ 0 Czy dobrze myślę?

Adamm: tak, rozwiąż nierówności i po sprawie

Jan: Okej, jakby mi ktoś mógł jak rozwiązać tą nierówność po prawej stronie bo troszkę się zapomniało... [(a−1)(a−2)−(a+1)]/(a+1)<=0 Co z tym?

Jan: Czy wyjdzie przedział a∊(−∞;1> ∪ <2;∞)

Adamm: nie

Jan: A jaki powinien wyjść z tego ^{a2 −3a+2}_a+1 ≤ 1 ?

Jan: no chwila... ^{a2 −3a +2} _a+1 −1 ≤ 0 ^{(a−2)(a−1)}_a+1 − ^a+1_a+1 ≤ 0 ^{(a−2)(a−1)(−a−1)}_a+1 ≤ 0 (a−2)(a−1)(−a−1)(a+1) ≤ 0 miejsca zerowe to : −1;1;2 Gdzies tutaj mam błąd?

Jan: Okej to zadanie ogarnąłem powoli, raczej jest dobrze. Pozostało jeszcze jedno i zarazem ostatnie. zad3. Naszkicuj wykres funkcji f(x) = 2sinx − √1−cos²x w zbiorze x∊ <π;2π> Ja to robie tak: f(x) = 2 sinx − |sinx|

	⎧	2sinx − sin x dla x≥0
f(x) =	⎨
	⎩	2sinx +sinx dla x<0

	⎧	sinx dla x≥0
f(x) =	⎨
	⎩	3sinx <0

Czy jest to poprawnie rozwiązane? Jak teraz narysować ten wykres?

Adamm: f(x)=2sinx−|sinx| jest ok ale dalej jest źle

Jan: To nie z definicji wartości bezwzględnej?

Adamm: tak, z definicji źle ją użyłeś

Jan: hmm.. wskaż mi błąd

Jan: oczywiście tam miało być 3 sinx dla x< 0

Jan: O ten błąd chodziło?

Adamm: nie

Jan: Wskaż drogę!

Jan: Serio nie mam pojęcia co jest źle

Adamm: rozpisz sobie |sinx| zgodnie z definicją wartości bezwzględnej

Jan:

	⎧	sinx dla sinx≥0
f(x) =	⎨
	⎩	−sinx dla sinx<0

Adamm: teraz już wiesz o co chodziło?

Krzysiek: nie x>0 tylko sinx >0

Jan: Tylko jak to narysować? Mam narysować sinusa w przedziale <π;2π> a następnie wybrać te elementy które są większe bądź równe 0? A potem tak samo narysować 3sinx w tym samym przedziale i wybrać elementy mniejsze od zera?

Adamm: możesz tak zrobić, jasne

Jan: Adamm wielkie dzięki za pomoc!

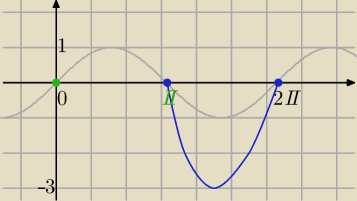
Mila: 3) f(x)=2sinx−√1−cos²x i x∊<π,2π> f(x)=2sinx−|sinx| i x∊<π,2π>⇔|sinx|=−sinx f(x)=3sinx na rysunku masz szkic