Wyznaczanie pochodnych itp Dudek: Witam mam tutaj kilka zadań dla mnie bardzo trudnych z góry dziękuje za pomoc w ich rozwiązaniu 1. Rozwiąż równanie, którego lewa strona jest sumą szeregu geometrycznego.

	x2		x3		x4		3x−1
a) x +		+		+		+ ... =
	2		4		8		3

	x2−2x−35		√x+3−1
2.A) lim x→7		B) kim x→−2
	x3−4x2−21x		2x+4

	1
C) kim x→2−
	√2−x

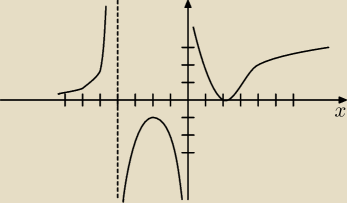
3. Na podstawie wykresu funkcji y = f(x) określ jej dziedzinę, zbiór wartości, miejsca zerowe, przedziały, w których funkcja przyjmuje wartości dodatnie (ujemne), przedziały monotoniczności, granice funkcji na końcach przedziałów określoności, równania asymptot oraz liczbę rozwiązań równania f(x) = m w zależności od wartości parametru m (mam nadzieję że cokolwiek widać na tym rysunku.... 4. wyznacz pochodną funkcji. Podaj dziedzinę D funkcji i dziedzinę D' jej pochodnej.

	3
A) f(x) = −3x4 − √7 B) f(x) = −		C) f(x) = (x2−1) ( 4x+5)
	5x5

	x
D) f(x) =
	2x−3

powrócony z otchłani: 1) lewa strona to suma nieskonczonego ciagu geometrycznego o a₁ = x²/2 ; q = x/2 Warunek na q rozwiazujesz po czym stosujesz wzor nanieskonczona sume ciagu geometrycznego

powrócony z otchłani: Skoro nie potrafisz policzyc granic i pochodnych to widac nie uwazales na zajeciach ... zajrzyj do teorii podanej na tej stronie. Masz tam podane przyklady wraz z rozwiazaniem

powrócony z otchłani: Dziedzina = wszystko poza asymptotami pionowymi Zbior wartosci = wszystko poza przedzialem (wierzcholek tej paraboli ; 0)

Dudek: a a₁ to nie jest po prostu x? tak czy inaczej teraz musze obliczyć sumę a później z tego x?

Dudek:

	a1
S1 =		istnieje jeżeli −1<q<1 czyli
	1−q

x		x
	< 1 ⋀		>−1
2		2

x		x
	−1<0 ⋀		+1>0
2		2

i nie wiem co dalej

Jerzy: x ∊ ( −2;2) Dalej...

x		3x − 1		2x		3x − 1
	=		⇔		=
1 − x/2		3		2 − x		3

Dudek: ale skąd się wzięło to x ∊ (−2;2) potem rozumiem że to już podstawienie do wzoru na sumę

Jerzy:

x
	< 1 ⇔ x < 2
2

x
	> − 1 ⇔ x > − 2
2

x ∊ (−2;2)

Dudek: i teraz muszę obliczyć z tego wzoru na sumę x i to jest odpowiedź na to zadanie ?

Jerzy: Rozwiąząć ostatnie równanie i wyniki skonfrontować z założeniem.

Jerzy: 4) a) f'(x) = −12x³

	3*25x4
b) f'(x) =		= ....
	25x10

c) f'(x) = 2x(4x + 5) + (x² − 1)*4 = ...

	2x − 3 − x*2
d) f'(x) =
	(2x − 3)2

Dudek: podpowie mi ktoś jak mam to równanie rozwiązać?

Jerzy: 6x = (2 − x)(3x − 1)

Dudek: no i co dalej ?

Dudek: pomógłbymi ktoś jeszcze z drugim zadaniem (oczywiście tam wszędzie ma być "lim" i może jak skończyc to pierwsze zadanie

powrócony z otchłani: Dudek ... na jakim poziomie edukacji jestes?

Dudek: 3 technikum

Dudek: taaa mam "drobne" zaległości

yht: dokończenie zadania 1 6x = (2−x)(3x−1) 6x = 6x−2−3x²+x 3x²+6x−6x−x+2=0 3x²−x+2=0 Δ=1−4*3*2 = 1−24 = −23 Δ < 0 Równanie sprzeczne, brak rozwiązań Zad. 2 A) x²−2x−35 Δ = (−2)²−4*1*(−35) = 4+140 = 144 → √Δ = 12

	2−12
x1 =		= −5
	2

	2+12
x2 =		= 7
	2

x²−2x−35 = (x+5)(x−7) x³−4x²−21x = x(x²−4x−21) Δ = (−4)²−4*1*(−21) = 16+84 = 100 → √Δ = 10

	4−10
x1 =		= −3
	2

	4+10
x2 =		= 7
	2

x³−4x²−21x = x(x+3)(x−7)

	x2−2x−35		(x+5)(x−7)
limx→7		= limx→7		=
	x3−4x2−21x		x(x+3)(x−7)

	x+5		7+5		12		6
= limx→7		=		=		=
	x(x+3)		7*(7+3)		70		35

B)

	√x+3−1		(√x+3−1)*(√x+3+1)
limx→−2		= limx→−2		=
	2x+4		(2x+4)(√x+3+1)

	(√x+3)2−12		x+3−1
= limx→−2		= limx→−2		=
	2(x+2)(√x+3+1)		2(x+2)(√x+3+1)

	x+2		1		1
= limx→−2		= limx→−2		=		=
	2(x+2)(√x+3+1)		2(√x+3+1)		2(√−2+3+1)

	1		1		1
=		=		=
	2(√1+1)		2(1+1)		4

C)

	1		1		1
limx→2−		= limx→1.99999...		=		=
	√2−x		√2−x		√2−1.99999...

	1
		= +∞
	√0.000001