Wyznacz wspólrzędne wierzchołków trójkata beti19: Wyznacz współrzędne wierzchołków trójkąta A'B'C', który jest obrazem trójkąta ABC w symetrii względem początku układu współrzędnych, wiedząc, że A=(−3,4), B=(1,6) i C=(4,−2). Ponadto oblicz pole i obwód każdego z tych trójkątów. wyznaczam współrzędne wzg. Soo ABC = A'B'C' A'= (3,−4) B'= (−1,−6) C'= (−4,2) i dalej proszę o pomoc..........

Jerzy: Rachunek wektorowy znasz ?

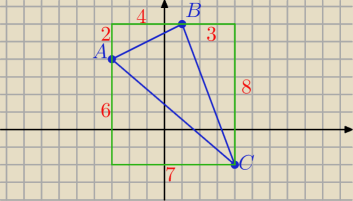
Janek191: I AB I = √4² + 2² = √20 = √4*5 = 2√5 I BC I = √3² + (−8)² = √73 I AC I = √7² + (−6)² = √85 Obwód Δ_ABC L = 2√5 + √73 + √85 Obwód Δ_A'B'C' jest taki sam. → AB = [ 4, 2] → AC = [ 7, − 6] więc pole Δ_ABC → → P = 0,5 I det ( AB, AC ) I = 0,5*I 4*(−6) − 2*7 I = 0,5* I − 38 I = 19 Pole trójkąta A'B'C' jest takie same. =============================== II sposób : P = 8*7 − 0,5*(8*3 + 4*2 + 6*7) = 56 − ( 12 + 4 + 21) = 56 − 37 = 19 =======================================================

beti19: bardzo Ci dziękuje Janek191 − zastanawiam mnie jedynie sposób w jaki obliczyłeś pole trójkąta ? czy ja czasem nie potrzebuję do obliczenia pola − wysokości tego trójkata ? czy ja nie mam czasem obliczyć odległość punktu B' od AC ?

Jerzy: Pole trójkąta , to połowa długości wektora bedącego iloczynem wektorowym wektorów AB i AC.