Ambitne zadania(tak mi sie wydaje). Bardzo prosze o wsparcie :P Ergo: Pare zadan zeby nie bylo ze nie probowalem i zeby latwiej bylo mi pomoc dodaje moje obliczenia : Prosze o pomoc 1)Wyznacz wszystkie pary liczb calkowitych (x,y) ktore spelniaja rownanie: (2x−y+1)(x−y+1)=7 moje zalozenia: 2x−y+1=1 i x−y+1=7 lub 2x−y+1=7 i x−y+1=1 jednak w odpowiedziach sa jeszcze dwie pary liczb:( jakich warunkow mi zabraklo?

	π		3π
2) Oblicz cos		+cos		. Wykorzystaj wzor :cos3α=cosα(4cos2α−3)
	5		5

moje obliczenia (nie wiem czy dobry kierunek obralem) :

	π5+3π5		π5−3π5
2cos		+cos
	2		2

	2π		−π
2cos		*cos
	5		5

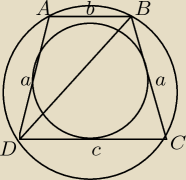
niestety nie wiem co dalej 3)Trapez rownoramienny o przekatnej dlugosci 13 cm i obwodzie rownym 48 cm jest opisany na okregu. Oblicz dlugosc promienia okregu wpisanego w ten trapez i dlugosc promienia okregu opisanego na tym tapezie. hmmm mam problem... 2a+b+c=48 b+c=2a |DB|=13

Godzio: 1) np takich: 2x−y+1 = −1 i x−y+1 = −7 lub 2x−y+1 = −7 i x−y+1 = −1

Godzio: 2) nie mam pojęcia ale zaraz nad 3 posiedze :

Ergo: okej dziekuje

Ergo: ooo ja 1 faktycznie.. czyli jednak mialem racje ze zadania ambine

Ergo: odswiezam

Ergo: ponownie

Ergo: ktos pomoze?

Ergo: ...:<

paziówna:

	π		3π
2) patrz: cos3*α = cos3α ⇔ cos3*(		) = cos(		)
	5		5

więc zaczynasz od podstawienia ze wzoru na cos3α:

	π		π		π		π		π
cos		+ cos		(4cos2		− 3) = cos		(1 + 4cos2		− 3) = ...
	5		5		5		5		5

Ergo: ehhh =D dzieki paziowna. jeszcze 3 zostalo

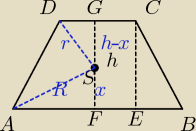
paziówna: 3) a, b, c, d, h > 0 L = 48 cm = 2a + b + c |DB| = |AC| = d = 13 jeśli okrąg jest opisany na trapezie, to (z własności): 2a = b + c wstawiasz do równania na obwód: 48 = 2a + 2a ⇒ a = 12 b + c = 12 ⇒ c = 12 − b (na moim rysunku) ΔACE:

	c − b		b + c
|AC|2 = |CE|2 + |AE|2 (|AE| = c −		=		)
	2		2

	b + c
d2 = h2 + (		)2
	2

	12
h2 = 132 − (		)2
	2

h² = 169 − 36 = 133 h = √133 jeśli okrąg jest wpisany i opisany na trapezie równoramiennym, środki tych okręgów pokrywają się (tutaj: pkt S) i teraz, często myk stosowany w tego typu zadaniach: dzielę wysokość na dwie długości względem pkt−u S. jeden nazywam x, drugi (h − x). rozpatruję dwa trójkąty: ΔAFS i ΔDSG |AS| − promień okręgu opisanego |DS| − promień okręgu wpisanego

	b		c
r2 = (h−x)2 + (		)2 ∧ R2 = x2 + (		)2
	2		2

x powinno się skrócić.

paziówna: to chyba nie jest pełne rozwiązanie, bo chyba do tego układu równań potrzebujesz konkretnie b i c...

Ergo: dzieki za poswiecony czas i pomoc

Ergo: poziom trudnosci tego zadania jest lekko przesadzony rozumiem ze to sa zbiorki z arkuszami maturalnymi ale bez przesady. Na prawdziwej maturze rozszerzonej nie ma tak rozbudowanych zadan

Ergo: mam na mysli tylko zad. 3 reszta jest w porzadku

paziówna: ΔEBC:

	c − b
a2 = h2 + (		)2
	2

	12 − b − b
169 − 133 =		)2
	2

36 = (12 − b)² 6 = 12 − b b = 6 c = 6....zdecydowanie coś się nie zgadza

Eta: Pomagam zad. 3)

Ergo: ok niestety musze isc ale jutro na 100 procent obejrze i przeanalizuje. Dzieki wszystkim za pomoc

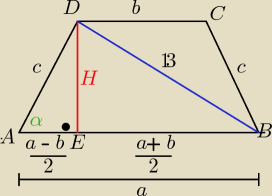
Eta: Moje oznaczenia: a, b −− dł. podstaw c −−− dł. ramion d=13 −−− dł. przekątnej

	h
r −− dł. prom. okręgu wpis. r=
	2

R −− dł. prom. okręgu opisanego ( okrąg opisany na trapezie jest tym samym okręgiem opisanym na ΔABD

	IBDI
więc		= 2R −−− ze wzoru sinusów
	sinα

	13
to R=
	2sinα

z warunków zad. a+b+2c = 48 i 2c= a+b => a+b= 24 to c = 12

	a+b
zatem		= 12
	2

z ΔEDD h² = IBDI² − IBEI²=169 − 144 = 25 => h= 5 to r=2,5

	h		5
teraz sinα=		=
	c		12

	13
więc R=		=.........
	2sinα

Bogdan: Zadanie 2.

	π		3π		2π		π		π   2sin   5
cos		+ cos		= 2cos		cos		*		=
	5		5		5		5		π   2sin   5

	π   π   2π   2sin cos *2cos   5   5   5
=		=
	π   2sin   5

	2π   2π   2sin cos   5   5		4π   sin   5
=		=		=
	π   2sin   5		π   2sin   5

	π   sin(π − )   5		π   sin   5		1
=		=		=
	π   2sin   5		π   2sin   5		2