Największa wartość i najmniejsza
misiek99: f(x)=4x/1+x
2 Wyznacz wartości najmniejszą i największą funkcji f w podanym przedziale
<−3;3>.
Z góry dziękuje

5 cze 20:15
kochanus_niepospolitus:
1) sprawdzasz dziedzinę (czy funkcja ciągła w podanym przedziale)
2)
f(−3) =

f(3) =

f'(x) = ...
f'(x) = 0 ⇔ x
1 =

jeżeli x
1∊(−3,3) to liczysz f(x
1) =

porównujesz wartości
5 cze 20:22
kochanus_niepospolitus:
wskazówka ... będą dwa ekstrema (i jeden punkt przegięcia
Patrz −−− funkcja jest nieparzysta

5 cze 20:23
misiek99: skąd się wzieło f'(x)=0

?
5 cze 21:02
piotr: | | 4 (−1 + x2) | |
f'(x) = − |
| |
| | (1 + x2)2 | |
f'(x) = 0 ⇔ x = −1 ∨ x = 1
f(−3) = −6/5
f(−1) = −2
f(1) = 2
f(3) = 6/5
5 cze 21:42
piotr:
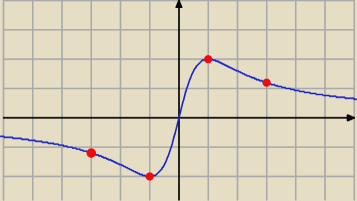
5 cze 21:44
kochanus_niepospolitus:
f'(x0) = 0 <−−− jest to warunek konieczny (ale nie wystarczający) aby funkcja f(x) posiadała
ekstremum lokalne w punkcie x0)
5 cze 21:46
Adamm: warunek konieczny jest taki
f'(x0)=0 lub f'(x0) nie istnieje
zazwyczaj nie wspomina się o tym drugim warunku, a szkoda
5 cze 21:48
Adamm: raczej o drugiej części tego warunku
5 cze 21:49
piotr: wartości najmniejszą i największą w przedziale domkniętym (w którym jest ciągła i
różniczkowalna) funkcja może przybierać na końcach przedziału lub w punktach gdzie f'(x)=0
5 cze 21:59
Adamm: ważne jest też to że funkcja taka w przedziale domkniętym zawsze posiada
wartość największą i najmniejszą
5 cze 22:04

 f(3) =
f(3) =  f'(x) = ...
f'(x) = 0 ⇔ x1 =
f'(x) = ...
f'(x) = 0 ⇔ x1 =  jeżeli x1∊(−3,3) to liczysz f(x1) =
jeżeli x1∊(−3,3) to liczysz f(x1) =  porównujesz wartości
porównujesz wartości

 ?
?
