Zbadaj monotoniczność nieskończonego ciągu awww: Jak zbadać monotoniczność ciągów rekurencyjnych? a) a₁=−8

	1
an+1=		an
	2

b) a₁=1 a_n+1=−3a_n

'Leszek: Sa to ciagi geometryczne a) q= 1/2 , a₁ = −8 , a_n = − 8 * (1/2)ⁿ⁻¹ Oblicz a_n+1 − a_n = ...... b) q = − 3 , a₁ = 1 , a_n = ( − 3)ⁿ⁻¹

awww: Oraz od razu się spytam o to czy dobrze rozwiązałem ten przykład: a_n= −n²+6n−5 dla n<4 lub n+1 dla 4≤n≤10 a_n+1= −(n+1)²+6(n+1)−5= −n²−2n−1+6n+6−5= −n²+4n dla n<4 lub (n+1)+1= n+2 a_n+1−a_n= −n²+4n+n²−6n+5= −2n+5 maleje(?) dla drugiego przedziału a_n+1−a_n= n+2−n−1=1 >0 rośnie dla drugiego przedziału w zbiorku w odpowiedziach jest po prostu napisane że ciąg rosnący

awww: Niestety ale nie miałem jeszcze ciągów geometrycznych, nie ma innego sposobu na zbadanie monotoniczności tych 2 pierwszych ciągów?

Mila: 1) a₁=−8

	1		an+1		1
an+1=		an⇔		=		⇔
	2		an		2

a_n jest ciągiem geometrycznym

	1
q=
	2

	1
an=−8*(		)n−1
	2

Teraz odpowiedz na pytanie 2) rozwiązuj podobnie

Mila: 18:52 I sposób− ponieważ masz tylko 10 wyrazów w ciągu to oblicz wartości wg wzorów . II sposób skorzystaj z własności funkcji kwadratowej i liniowej a) f(n)= −n²+6n−5 dla n<4 g(x)=−x²+6x−5 parabola skierowana w dół x_w=3 zatem dla x≤3 g(x) rosnąca⇒f(n) rosnąca dla n=1,2,3 b) s(n)=n+1 dla n∊<4,10> g(x)=x+1 rosnąca dla każdego x∊R⇒s(n) rosnąca dla n∊<4,10> Za chwilę (1 i 2) zadanie

Mila: 1)

	1
a2=		a1
	2

	1		1		1		1
a3=		a2=		*(		a1)=(		)2*a1
	2		2		2		2

	1		1		1		1
a4=		a3=		*(		)2*a1=a1*(		)3
	2		2		2		2

....

	1
an=a1*(		)n−1
	2

	1
an=−8 *(		)n−1
	2

Z własności funkcji wykładniczej:

	1
y=(		)n−1− funkcja malejąca
	2

	1
y=−8*(		)n−1− funkcja rosnąca
	2

awww: Wielkie dzięki Mila, ale czy mógłbyś/mogłabyś powiedzieć gdzie mam błąd(?) w przykładzie z 18:52? Wychodzi mi że a_n+1−a_n= −2n+5, więc to teoretycznie powinno maleć. Tak wgl to się teraz pogubiłem czemu zapisujemy a_n+1, a nie a_n−1 jeśli przy przesuwaniu funkcji w prawo to "odejmujemy".

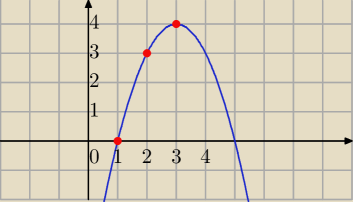
Mila: a_n= −n²+6n−5 dla n<4 Tu chodzi o trzy wyrazy: a₁, a₂ ,a₃ to po co takie rachunki robisz? a₁=0, a₂=3 ,a₃=4 −−−−−−−−−−− masz obliczone: a_n+1−a_n=−2n+5 −2n+5>0 ? −2n>−5

	5
n<		⇔n∊{1,2}
	2

a₁<a₂ i nie wiadomo co z a₃ ? musisz obliczyć a₂ i a₃ i dopiero wnioski. a_n=−n²+6n−5 Funkcja y=−x²+6x−5 nie jest monotoniczna 2) Odejmujesz od następnego wyrazu wyraz poprzedni.