zadnie z ciągów Bidek: Dla jakiej wartości parametru a ciąg jest zbieżny ?

	⎧	3n( 3√n2 + n −n ) dla n parzystych
an=	⎩	a−3 dla n nieparzystych

Nie za bardzo rozumiem, mam pokazać dla jakiego parametru a ciąd ma ganicę skończoną ? Jesli nawet tak to i tak nie za bardzo rozumiem bo to est ciag zlozony z dwoch ktos pomoze ?

Adamm: a_2n+1=a−3 jeśli ciąg ma mieć skończoną granicę to granica podciągu a_2n musi wynosić a−3

Bidek: Niestety nie rozumiem, dlaczego tak ma być ?

kochanus_niepospolitus: aby ciąg a_n był zbieżny (czyli posiadał granicę 'g' ) to każdy podciąg ciągu a_n musi być zbieżny do granicy g (Tw. Heinego się kłania).

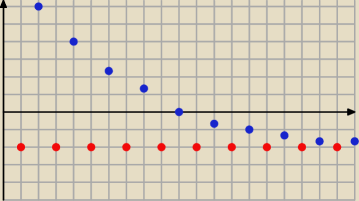
kochanus_niepospolitus: Ilustracja czerwone reprezentuje podciąg stały (a−3) niebieskie reprezentuje podciąg 3n(³√n²+n − n Uwaga ... wartości dałem 'przypadkowe' nie sugeruj się nimi przy rozwiązywaniu Jak widzisz ... ciąg ten będzie miał granicę tylko wtedy ... gdy 'niebieskie kropki' będą dążyć do czerwonych ... czyli do wartości a−3

Bidek: No ale nadal troche nie rozumiem xD

	⎧	6n (3√4n2 +2n − 2n dla n parzystych
a2n=	⎩	a−3 dla n nieparzystych

prawda ? więc co mi to daje xD po 2 to granica z wzoru dla n paryztych to nieskonczonosc

Bidek: czyli a−3 musi byc granica ciagu dla n parzystych ?

kochanus_niepospolitus: tak Blade −−− (a−3) ma być granicą podciągu {a_2n}

Bidek: wszytsko rozumiem przez ta ilustacje, zarąbiste kochanus_niepospolitus wiec problem pozostaje tylko taki ze granica tamta to +∞

Bidek: I jeszcze jedno pytanie dlaczego nie wystarczy ze a−3 ma byc granica 3n ( ³√n² +n +−n ) ? tylko musi byc granica podciagu a2n ?

kochanus_niepospolitus: jak już to: lim_n−>∞ 3n(³√n²+n −n) = −∞

kochanus_niepospolitus: ale przecież wyrazy 3n(³√n²+n − n) SĄ WYRAZAMI które są wyrazami także podciągu a_2n

Bidek: ale przecież wyrazy 3n(³√n²+n− n) SĄ WYRAZAMI które są wyrazami także podciągu a2n no tak zgadzam sie w 100% ale czemu nie mógłbym tego robić po prostu dla an tylko mam robic dla a2n a nastpnie, skoro granica to −∞ wiec tak jakby to a tez musi byc −∞ ?

kochanus_niepospolitus: a jak (najlepiej z definicji) obliczysz granicę ciągu a_n Słucham ja Ciebie

kochanus_niepospolitus: przedewszystkim ... jeżeli wychodzi lim a_2n = −∞ ... to znaczy, że podciąg a_2n jest rozbieżny ... więc na mocy tw. Heinego zostało udowodnionie (niewprost) że ciąg a_n nie jest zbieżny

Bidek: Dobra już rozumiem wszystko może nauczyciel sie pomylil układając to zadanie i dlategi nie ma granicy wlasciwej tam

Bidek: Wielkie dzięki

kochanus_niepospolitus: najproawdopodobniej miało być 3(³√n³+n−n)