w jakim stosunku parabola y2 =2x dzieli pole koła x2 +y2 =8
ala: w jakim stosunku parabola y2 =2x dzieli pole koła x2 +y2 =8
Rozwiązałam równanie.
Wyszło mi że A(2;2), B(2,−2); C (0;
√8)
Pk= 8π
a co dalej? niestety nie miałam jeszcze całek a zadanie do zrobienia jest..

4 cze 20:13
Adamm: a miałaś granice?
4 cze 20:17
ala: tak
4 cze 20:18
Adamm: znasz wzór na sumę kolejnych kwadratów liczb naturalnych?
12+22+...+n2=... ?
4 cze 20:40
Adamm: a może znasz twierdzenie Stolza?
4 cze 20:43
ala: 12+22+...+n2=n(n+1)(2n+1)/6 tylko co tu do czego podstawić?
4 cze 21:03
Adamm: aproksymujesz pole pod wykresem paraboli prostokątami
http://eduinf.waw.pl/inf/alg/004_int/0002.php
pole otrzymasz jeśli weźmiesz to wszytko do granicy
dlatego napisałem czy znasz wzór na sumę kolejnych kwadratów liczb naturalnych,
będzie on potrzebny przy granicy
jak policzysz pole pod wykresem paraboli to dalej już prosto
4 cze 21:08
Mila:
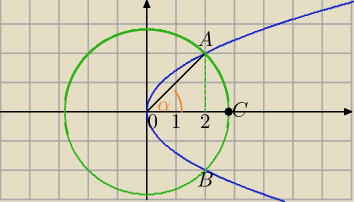
y
2 =2x
x≥0
y=
√2x lub y=−
√2x
x
2+y
2=8
α=45
o
| | 45 | |
Pwycinka koła A)C= |
| *π*8=π |
| | 360 | |
| | 2 | | 1 | |
Podcinka koła=0∫2(√2*√x−x) dx=[√2* |
| *x3/2− |
| x2]02= |
| | 3 | | 2 | |
| | 2√2 | | 1 | | 2 | |
= |
| *23/2− |
| *22= |
| |
| | 3 | | 2 | | 3 | |
| | 2 | | 4 | |
Pm=2*( |
| +π)= |
| +2π −pole mniejszej części koła |
| | 3 | | 3 | |
P
koła=8π
4 cze 21:11

 y2 =2x
x≥0
y=√2x lub y=−√2x
x2+y2=8
α=45o
y2 =2x
x≥0
y=√2x lub y=−√2x
x2+y2=8
α=45o