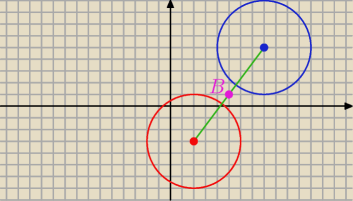
Geometria analityczna K: Dany jest okrąg o: x²+y²−4x+6y−3=0. Wyznacz równanie okręgu o₁ będącego obrazem okręgu o w symetrii środkowej względem punktu: B(5,1) Moje obliczenia: −2a_o=−4 a_o=2 −2b_o=6 b_o=−3 S_o(2,−3) r²=a²+b²−C=4+9+3=16 r=4 (bo musi być dodatni) Wyznaczam jakiś szukany punkt P(x, y) leżący na prostej k przecinającej punkt S_o oraz B.

	|SP|
|SB|=|PB| ⇒		=|PB|
	2

xp+2
	=5
2

x_p=8

yp−3
	=1
2

y_p=−1 I tutaj mi się nie zgadza nawet z rysunkiem. Gdyby w równaniu zamiast minusa był plus ⇒

	yp+3
		=5 Wtedy wszyściutko się zgadza i wynik wychodzi P(8,5) ⇒ (x−8)2+(y−5)2=16
	2

Proszę o pomoc w znalezieniu błędu.

Eta: B(5.1) i S(2,−3) , r=4 S^'(x_S^',y_S^') r^'=r=4 x_S^'=2x_B−x_S=8 i y_S^'=2y_B−y_S= 5 S^'(8,5) o^': (x−8)²+(y−5)²=16

Janek191: x² + y² − 4 x + 6 y− 3 = 0 ( x − 2)² − 4 + ( y + 3)² − 9 − 3 = 0 (x −2)² + ( y + 3)² = 4² S = ( 2 , − 3) r = 4 B = ( 5, 1) więc S' = ( x ' , y')

2 + x'		− 3 + y '
	= 5 i		= 1
2		2

2 + x' = 10 i − 3 + y' = 2 x ' = 8 y ' = 5 Równanie okręgu w symetrii środkowej względem B ( x − 8)² + ( y − 5)² = 16 =====================

K: Jezu przepraszam za ten akt głupoty, nie wiem dlaczego nie zmieniłem znaku przenosząc −3 na drugą stronę.

Mila: o: x²+y²−4x+6y−3=0 (x−2)²−4+(y+3)²−9−3=0 (x−2)²+(y+3)²=16 S=(2,−3) , r=4 Obrazem okręgu w symetrii jest okrąg o tym samym promieniu. Punkt B=(5,1) jest środkiem odcinka SS' S'=(x,y)

	2+x		−3+y
5=		i 1=		/*2
	2		2

10=x+2 i 2=−3+y x=8 i y=5 S'(8,5) − środek nowego okręgu Równanie okręgu: (x−8)²+(y−5)²=16

Eta:

K: Rachunki trudniejsze od częsci merytorycznej