przebieg zmienności Adam: x3/(3−x2) − przebieg zmienności funkcji

Adamm: zaczynaj, każdy ma inny sposób na badanie przebiegu zmienności funkcji dodatkowo, zajmuje to wiele czasu

dociekliwy: 1. Dziedzin 2.Pochodna

Adam: nie wiem na podstawie czego zrobić tabelę i jak narysować

dociekliwy: Daj sobie siana z tabelą.

Adam: muszę na zaliczenie

Mila:

	x3
f(x)=		taka funkcja?
	3−x2

Adam: tak

Mila: 1) Dziedzina: 3−x²≠0⇔ x≠√3 i x≠−√3 D=R\{−√3,√3} 2) miejsca zerowe: x³=0⇔ x=0 3) Granice na krańcach dziedziny

	x3		x2*x
a) limx→∞		=limx→∞		=
	3−x2		3x2−1

	x
=limx→∞		=−∞
	3x2−1

	x3
b) limx→−∞		=∞
	3−x2

	x3		3√3
c) limx→√3+		=[		]=−∞
	3−x2		0−

	x3		3√3
limx→√3−		=[		]=∞
	3−x2		0+

x=√3− asymptota pionowa

	x3		−3√3
limx→−√3+		=[		]=−∞
	3−x2		0+

	x3		−3√3
limx→−√3−		=[		]=∞
	3−x2		0−

x=−√3 asymptota pionowa d) asymptota ukośna y=ax+b

	f(x)
a=lim x→±∞
	x

	x3		x2
a=limx→±∞		=limx→±∞		=−1⇔
	x*(3−x2)		3−x2

a=−1 b=lim _x→±∞(f(x)−ax)

	x3		x3+x*(3−x2)
b=limx±∞(		+x)=limx±∞		=
	(3−x2)		3−x2

	3x
=limx→±∞		=0
	3−x2

y=−x asymptota ukośna 4) f'(x) = Licz pochodną za pół godziny będę.

dede: f'(x)= (9x²−x⁴)/ (3−x²)²

Mila: dede,Ty jesteś Adam?

dede: tak

Mila:

	x2*(9−x2)
f'(x)=
	(3−x2)2

5) Monotoniczność: f'(x)>0⇔9−x²>0 i x≠√3 i x≠−√3 (3−x)*(3+x)>0 parabola skierowana w dół x∊(−3,3)\{−√3,√3}⇔ f(x)↗ (rosnąca ) w przedziałach (−3, −√3) oraz (−√3,√3) oraz (√3,3) Malejąca w przedziałach: (−∞, −3) oraz (3,∞) dla x=−3 f(x) ma min . lokalne ( pochodna zmienia znak z ujemnego na dodatni przy przejsciu przez x=−3)

	−27		9
fmin=f(−3)=U{(−3)3}{(3−9)=		=
	−6		2

	27		9
fmax=f(3)=		=−
	−6		2

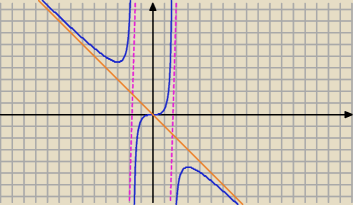
6) Mając te informacje szkicujesz wykres kreślisz asymptoty, zaznaczasz m. zerowe, maks. i min., patrzysz na granice i monotoniczność.

dede: a jak zrobić tabelkę?

Mila: Popatrz do notatek, nie wiem, jak teraz robicie tabelki.