przebieg zmienności funkcji
Az: hej, potrzebuję przebieg zmienności dwóch funkcji:
a) x4−6x2−6x
b) x3/(3−x2)
2 cze 14:27
Jerzy:
a)
Na początek:
1) Ustal dziedzinę
2) Policz pochodną
2 cze 14:28
Az: a) dziedzina R/(pierw. z 3 i − pierw z 3
b) R
pochodną też mam tylko nie wiem mogę liczyć potem asymptot bo wychodzi nieskończoność w b
2 cze 14:32
Jerzy:
Po kolei...
a)
D = ?
f'(x) = ?
2 cze 14:33
Az: D=R
f'(x)= 4x3−12x−6
2 cze 14:34
Jerzy:
Dobra... miejsca zerowe pochodnej ?
2 cze 14:35
Az: czyli do 0 przyrównać tak? i właśnie tu zaczyna się problem..
2 cze 14:36
Jerzy:
Sprawdź treść, po pierwiastki są nieciekawe.
2 cze 14:45
Az: wiem dlatego mam problem..już sprawdzałam..
2 cze 14:45
Jerzy:
W zadaniach na badanie funkcji rzadko sie zdarza,
aby juz sama pochodna sprawiała trudności.
2 cze 14:46
Az: wiem, podejrzewam ze jest błąd w zadaniu.. teraz się tylko upewniłam..
2 cze 14:48
Jerzy:
b)
D = ?
f'(x) = ?
2 cze 14:48
Az: D=R/(−p(3), p(3))
f'(x)= (9x2−x4)/(3−x2)2
2 cze 14:50
Jerzy:
Dobra ..teraz miejsca zerowe pochodnej.
2 cze 14:53
Az: 0 i 2,25
2 cze 14:55
Jerzy:
A skąd taki wynik ?
2 cze 14:58
Az: licznik ułamka porównałam do 0
2 cze 14:59
Jerzy:
No i ....
2 cze 15:00
Az: 0 i 0,5?
2 cze 15:03
Jerzy:
9x2 − x4 = 0 ⇔ x2(3 − x)(3 + x) = 0 ⇔ .... ?
2 cze 15:05
Az: 0,3,−3
2 cze 15:07
Jerzy:
Dobra ... teraz musisz ustalić jak zmienia się znak pochodnej w tych punktach
( znak pochodnej zależy tylko od znaku licznika , bo mianownik jest stale dodatni )
2 cze 15:08
Az: a jak to ustalić?
2 cze 15:11
Jerzy:
Słyszałaś coś o tzw. "wężyku" ?
2 cze 15:13
Az: chodzi o monotoniczność? w sensie np maksimum, minimum?
2 cze 15:13
Jerzy:
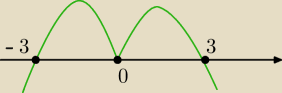
To jest wykres licznika pochodnej, jak zmienia znak w tych punktach ?
2 cze 15:17
Jerzy:
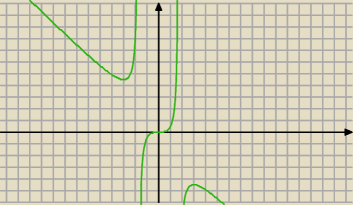
Tak wygląda wykres tej funkcji ( wyjściwej ) , ale musimy do niego dojść po kolei.
Na razie ustalamy ekstrema lokalne.
2 cze 15:20