bardzo prosze o pomoc Mateusz: Może ktoś pomoże. Mam problem z kilko zadaniami , więc jeśli ktoś miałby chwilkę czasu na to , żeby opisać krótko każde z nich, jak je rozwiązać, to byłbym niezmiernie wdzięczny. 1.Największą wartością funkcji f(x)=−1/2(x−4)²−2, gdy x∊<−2;0> jest −10. Prawda/Fałsz 2.Zbiorem wartości funkcji kwadratowej f jest przedział (−∞;−4> gdy f(x)=−4(x−4)²−4 . Prawda/Fałsz 3.Wyznacz wzór funkcji kwadratowej: a)najmniejszą wartość równą 5 funkcja przyjmuje gdy x=−2, oraz parabola, która jest wykresem funkcji f przecina oś y w punkcie (0,9) b)osią symetrii wykresu funkcji f jest prosta o równaniu x=10, punkt P(9,1) należy do wykresu funkcji f oraz Y_l =<0;+∞) c)x₁ =−3 x₂ = 5 u punkt (1,16) należy do zbioru funkcji f.

Mateusz: Może jednak ktoś?

po prostu Michał: 1) Dana funkcja to parabola, gdzie masz podana postac kanoniczna a(x−p)² + q (u Ciebie : a = − 1/2, p = 4, q = − 2) oczywiscie W(p,q) to wierzcholek. Badajac najwieksza wartosc funkcji w przedziale trzeba zrobic 3 rzeczy 1) sprawdzic wartosci funkcji na krancach badanego przedzialu, czyli tutaj f(−2) oraz f(0) 2) sprawdzic czy wierzcholek paraboli nalezy do badanego przedzialu (iksowa wierzcholka) 3) jesli nalezy to policzyc wartosc funkcji dla iksowej, czyli igrekowa wierzcholka Jednakze Ty juz wszystko masz podane odnosnie wierzcholka we wzorze funkcji, gdyz p = 4, q = 2 (oczywiscie p ≠ <−2;0>, bo 4 nie miesci sie w <−2;0>) zatem badamy jedynie na krancach przedzialu. zatem f(−2) = −1/2(−2−4)² − 2 = −1/2(36) − 2 = − 18 − 2 = − 20 f(0) = −1/2(0−4)² − 2 = −1/2(16) − 2 = − 8 − 2 = − 10 Co jest wieksze −10 czy − 20? Zatem odpowiedz −> najwieksza wartosc to ?

po prostu Michał: zad 2. Zbiorem wartosci funkcji kwadratowej o ujemnym wspolczynniku "a" tutaj a = − 4 bo f(x) = −4(x−4)² − 4 jest przedzial od (−∞;q> gdzie "q" to igrekowa wierzcholka. U nas p = 4, q = − 4 zatem odpowiedz?

po prostu Michał: zad 3. a) Dla argumentu x = − 2 wartosc funkcji, czyli f(−2) = 5 oraz parabola, przecina oś OY w punkcie (0,9) czyli dla x = 0, f(0) = 9 Zatem, skoro najmniejsza wartosc to 5, to znaczy ze parabola jest "uśmiechnięta" gdyż zbiór wartości idzie od <5;∞) (no bo 5 jest najmniej) stad juz wiadomo, ze q = 5, " p " tez jest znane, gdyz dla x = − 2 to te q = 5, zatem p = − 2 stad juz wiemy ze funkcja na pewno wyglada tak f(x) = a[x−(−2)]² + 5 czyli f(x) = a(x+2)² + 5 zeby obliczyc "a" podstawiamy punkt (0,9) gdyz nalezy on do wykresu funkcji. zatem 9 = a(0+2)² + 5 9 = 4a + 5 −−−> 4a = 4 −−−> a = 1 zatem wykres funkcji to f(x) = 1(x+2)² + 5 czyli f(x) = (x+2)² + 5 jest to postac kanoniczna, mozna sprowadzic do postaci ogolnej poprzez wymnozenie tego kwadratu czyli f(x) = (x²+4x+4) + 5 = x² + 4x + 9 W zaleznosci jaka postac potrzebujesz.

Mateusz: Dziękuję bardzo za poświęcony czas Michał, niewątpliwie Mi się to przyda i większość jest już dla Mnie jasna.

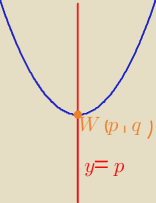
po prostu Michał: zad 3. b) osia symetrii funkcji kwadratowej jest prosta y = p (bo dokladnie w wierzcholku parabola dzieli sie na dwie czesci −> patrz rysunek) zatem skoro osia symetrii jest prosta x = 10, to wiadomo ze p = 10. Wiadomo rowniez, ze punkt P(9,1) nalezy do parabolii oraz, ze zbior wartosci to przedzial <0,∞) zatem jest to parabola usmiechnieta (ramiona do gory) gdyz najmniejsza wartosc to 0 zatem rownanie funkcji kwadratowej (jeszcze bez punktu P(9,1)) to y = a(x−10)² + 0 podstawiajac punkt P(9,1) mamy 1 = a(9−10)² 1 = a zatem ostateczny wzor funkcji to y = 1(x−10)² czyli y = (x−10)²

po prostu Michał: c) sprobujesz sam? wykorzystaj wiedze, ze wierzcholek lezy dokladnie pomiedzy miejscami zerowymi

	x1+x2
czyli p =
	2

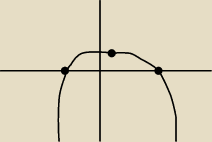
Mateusz: −3+5/2=2/2=1 a=−1 Tak?

Mateusz: y=−(x+3)(x−5)

po prostu Michał: (−3+5) / 2 = 2/2 = 1 (lepiej dac tam nawias) wynik ok

Mateusz: Dziękuję raz jeszcze Sprawdzilbys czy dobrze zrobilem te wykresy? a) f(x)=−2(x−1)²−2 b)f(x)=2x²−4x c)f(x)=−1/2(x+2)(x−3) http://screenshot.sh/oAkm6vjcPpvnv <−−−− wykresy

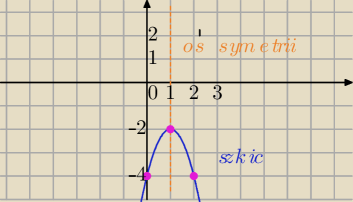
Mila: 1) f(x)=−2(x−1)²−2 W=(1,−2) Miejsca zerowe: −2(x−1)²−2=0 −2(x−1)²=2 /:(−2) (x−1)²=−1 brak miejsc zerowych f(0)=−2*1−2=−4

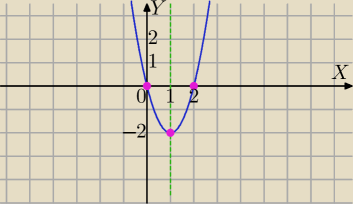
Mila: b)f(x)=2x²−4x

	4
xw=		=1
	4

y_w=2*1−4=−2 W=(1,−2) Miejsca zerowe 2x*(x−2)=0 x=0 lub x=2

Mila:

	1
c)f(x)=−		*(x+2)(x−3)
	2

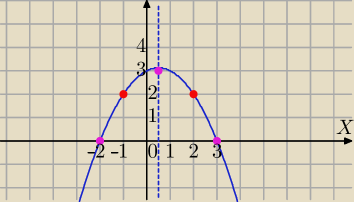
1) miejsca zerowe:

	1
−		*(x+2)(x−3)=0
	2

x+2=0 lub x−3=0 x=−2 , x=3

	−2+3		1
xw=		=
	2		2

	1		1		1		1		1		5		5		25
f(		)=−		*(		+2)*(		−3)=−		*		*−		=
	2		2		2		2		2		2		2		8

	1		25
W=(		,		)
	2		8

	1
f(−1)=−		*(−1+2)*(−1−3)=2=f(2)
	2

Mateusz: skąd wzięłaś f(−1) ?

Mila: Chciałam mieć dodatkowe punkty wykresu, wybór jest dowolny, oby tylko dobrze się liczyło.

Mateusz: Czyli mogę wybrac dowolne punkty , byle mieściły się w przedziale?

Mila: Nie masz przedziału, f(x) jest określona dla x∊R. Jeśli wybierzesz x=10 to trudno będzie narysować . Trzeba się kierować rozsądkiem.