Pytający:
"Prawie" ręcznie.
Liczba prostokątów w kracie rozmiaru mxn (m wierszy, n kolumn):
https://www.wolframalpha.com/input/?i=sum+a%3D1...m+(sum+b%3D1...n+((m%2B1-a)*(n%2B1-b)))
// prostokątów o wymiarach axb jest (m+1−a)(n+1−b) dla 1≤a≤m, 1≤b≤n
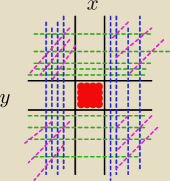
Liczba prostokątów w kracie rozmiaru mxn (m wierszy, n kolumn) zawierających kwadrat w wierszu
y i kolumnie x, 1≤y≤m, 1≤x≤n (patrz rysunek):
g(m,n,y,x)=
f(m,n)
−(
f(y−1,n)+
f(m−y,n)+
f(m,x−1)+
f(m,n−x))
+(
f(y−1,x−1)+f(y−1,n−x)+f(m−y,x−1)+f(m−y,n−x))
Szukana liczba prostokątów z zasady włączeń i wyłączeń:
f(7,7) // wszystkie prostokąty
−g(7,7,6,2) // prostokąty zawierające kwadrat (6,2)
−g(7,7,1,3) // prostokąty zawierające kwadrat (1,3)
−g(7,7,3,6) // prostokąty zawierające kwadrat (3,6)
+g(2,6,1,2) // prostokąty zawierające kwadraty (6,2) i (1,3), wiersze 1...6 scalamy do jednego
wiersza, podobnie kolumny 2...3 scalamy do jednej kolumny
+g(4,3,3,2) // prostokąty zawierające kwadraty (6,2) i (3,6), wiersze 3...6 scalamy do jednego
wiersza, podobnie kolumny 2...6 scalamy do jednej kolumny
+g(5,4,1,3) // prostokąty zawierające kwadraty (1,3) i (3,6), wiersze 1...3 scalamy do jednego
wiersza, podobnie kolumny 3...6 scalamy do jednej kolumny
−g(2,3,1,2) // prostokąty zawierające kwadraty (6,2) i (1,3) i (3,6), wiersze 1...6 scalamy do
jednego wiersza, podobnie kolumny 2...6 scalamy do jednej kolumny
=421
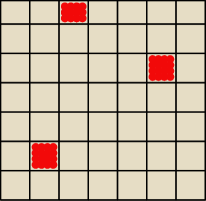Ile jest takich prostokątów które nie zawierają żadnych czerwonych kwadratów?
