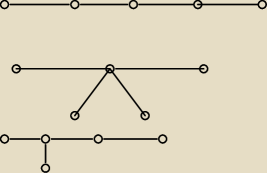
Podaj wszystkie grafy z twierdzenie Cayleya dla n=5 Qto: Podaj wszystkie grafy z twierdzenie Cayleya dla n=5 Mam takie coś jak wyżej. Nie wiem jak wyliczyć, że ma być to 125 kombinacji.

jc: Pierwszy typ: 120/2=60 Drugi typ: 5 trzeci typ: 120/2=60 razem 125

Pytający: 1.

5!
	=60 // połowa wszystkich permutacji, bo 1−2−3−4−5 jest izomorficzne z 5−4−3−2−1 itd.
2

	5 1
2.		=5 // wierzchołek środkowy (ten o stopniu 4) możemy wybrać na 5 sposobów

	5 1		4 1		3 1		5 1		4 1		3 2
3.		*		*		=		*		*		=60 // wierzchołek o stopniu 3 wybieramy na 5

sposobów, wierzchołek o stopniu 2 wybieramy na 4 sposoby, z pozostałych wybieramy albo

	3 1
wierzchołek o stopniu 1 sąsiadujący z tym o stopniu 2 na		=3 sposoby, albo wybieramy 2

	3 2
wierzchołki o stopniu 1 sąsiadujące z wierzchołkiem o stopniu 3 na		=3 sposoby (to ten

sam wybór, bez różnicy jak policzysz) 60+5+60=125