ciagi Wiktoria: Czesc ! mam zadania : 1.Dany jest niekończony ciąg liczbowy ( a_n ) określony wzorem a_n = (6n−6) / n+1. Wyznacz wszystkie naturalne dodatnie wyrazy ciągu ( a_n ) oraz zbadaj monotonniczność ciągu. 2.Ciąg a_n jest nieskończonym ciągiem geometrycznym, którego wyrazy spełniają warunek: {a₅ − a₁ =240 {a₄ + a₂ = 90 Oblicz pierwszy wyraz i iloraz tego ciągu. 3. Oblicz sume wszystkich liczb dwucyfrowych, które przy dzieleniu przez 4 dają reszte 2. Chodzi mi rownież o dobre wytlumaczenie jak robic takie zadania, a nie o same wyniki.

Wiktoria: Czy dobrze robie 2? a₁( q⁴ −1) =240 a₁q(q² +1) =90 a₁(q²−1)(q²+1) =240 a₁q(q²+1)=90 90(q² −1 )=240 90q²− 90 =240 90q²=330 q² =330/90

Wiktoria:

Wiktoria: halo

Wiktoria: :'(

Wiktoria: ktos wytłuaczy mi pierwsze zadanie?

Mila: 1)

	(6n−6)
an =
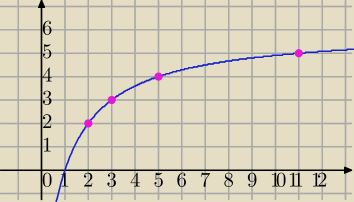
	n+1

6n−6		6n+6−6−6		6*(n+1)−12
	=		=		=
n+1		n+1		n+1

	12		12
=6−		>0 i (6−		) ∊N+
	n+1		n+1

D₁₂={1,2,3,4,6,12}− naturalne dzielniki liczby 12 a) n+1=1 , n=0 ∉N₊ b) n+1=2⇔n=1

	12
6−		=6−6=0∉N+
	2

c) n+1=3, n=2

	12
6−		=6−4=2 , a2 =2
	3

d) n+1=4⇔n=3

	12
6−		=6−3=3 ,a3=3
	4

e) n+1=6, n=5

	12
6−		=6−2=4 a5=4
	6

f) n+1=12, n=11

	12
6−		=6−1=5 , a11=5
	12

Odp. daj sama.

Mila: 2) a₁*q⁴−a₁=240 a₁*q³+a₁*q=90 −−−−−−−−−−−−−−− a₁*(q⁴−1)=240 a₁*q*(q²+1)=90 −−−−−−−−−−−−−−−−−−−−−− dzielę stronami

(q2−1)*(q2+1)		24
	=
q*(q2+1)		9

q2−1		8
	=
q		3

3*q²−3=8q 3q²−8q−3=0

	1
q=−		lub q=3
	3

licz a₁ i sprawdź , czy spełniają układ równań