Wektory - zadanie tekstowe K: Punkt A(0, −5) oraz D(−3, −1) są kolejnymi wierzchołkami trapezu równoramiennego ABCD którego osią symetrii jest prosta o równaniu x+2y=0. Oblicz współrzędne pozostałych wierzchołków oraz długość odcinka łączącego środki ramion tego trapezu.

	|−3−2|		5√5
Obliczam odległość punktu od prostej x+2y=0 ⇒ d=		=
	√5		5

	x
Chcę wyznaczyć prostą prostopadłą do prostej y=−		przechodzącą przez punkt D ⇒ a1*a2=−1
	2

	2
⇒ y=
	x

	2
No ale postać y=		jest lekko problematyczna i nie potrafie sobie wyznaczyć wzoru tej
	x

funkcji. Proszę o pomoc.

'Leszek: Prosta y = (−1/2)x , prosta do niej prostopadla to : y = 2x + b i D (−3,−1) podstaw i oblicz .

Eta:

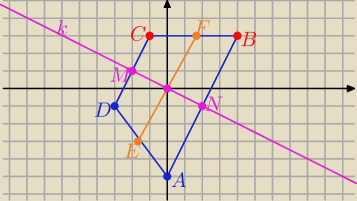
	1
k: y= −		x to DC: y=2(x−xD)+yD⇒ y=2x+5
	2

C jest symetryczny względem k Rozwiązując układ równań prostych k i DC otrzymasz M −−− który jest środkiem odcinka DC zatem wyznaczysz ................. C(−1,3) analogicznie wyznacz współrzędne punktu N bo prosta AB ⊥k i przechodzi przez A ....... Mając już wszystkie współrzędne punktów

	|AB|+|CD|
długość |EF|=		=........
	2

K: Prosta prostopadła do prostej k, przechodząca przez punkt D(−3, −1) ⇒ l :2x−y+5=0 podstawiam odległość punktu od prostej d=√5

	|2x−y+5|
√5=
	√5

2x−y=0 v 2x−y+10=0