Uzasadnij, że DE ⊥ CB oraz, że |DE| = 1/ 2 |CB|. matfizw: W trójkącie ABC o kątach <) C = 60◦ , <) B = 45◦ poprowadzono wysokość CD. Punkt D połączono odcinkiem ze środkiem E boku CB. Uzasadnij, że DE ⊥ CB oraz, że |DE| = 1/2 |CB|.

'Leszek: Zrob koniecznie rysunek ,wowczas : Kat CAB = 75°, kat ACD= 15° , kat DCB = 45° Czyli Δ CDB jest prostokatny rownoramienny , CD = DB , odcinek CD jest srodkowa do boku BC , jest jednoczesnie wysokoscia tego Δ CDB , czyli DE prostopadle do CB i DE= 0,5 CB

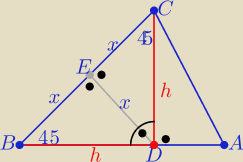
Eta: Objaśnione przez Leszek

'Leszek: Dzieki Eta , ja korzystam z komorki , wiec niewygodnie mi jest robic rysunki !