wykaż żę cde jest równoramienny
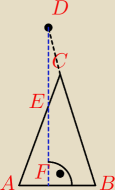
matfizw: Na przedłużeniu boku BC trójkąta równoramiennego ABC, w którym
|AC| = |BC|, odkładamy odcinek CD o długości krótszej niż odcinek
BC. Niech F będzie rzutem prostopadłym punktu D na podstawę AB,
a odcinek DF niech przecina ramię AC w punkcie E. Uzasadnij, że
trójkąt CDE jest równoramienny.
28 maj 13:19
Adamm:
no więc tak
|∡ABC|=α
wtedy |∡BDF|=90
o−α ponieważ w trójkącie kąty sumują się do 180
o
|∡ACB|=180
o−2α również z tego powodu
|∡DCE|=2α tego chyba nie muszę tłumaczyć
|∡DEC|=90
o−α również z powodu kątów w trójkącie
ma dwa kąty równe ⇒ jest równoramienny
28 maj 13:39
 no więc tak
|∡ABC|=α
wtedy |∡BDF|=90o−α ponieważ w trójkącie kąty sumują się do 180o
|∡ACB|=180o−2α również z tego powodu
|∡DCE|=2α tego chyba nie muszę tłumaczyć
|∡DEC|=90o−α również z powodu kątów w trójkącie
ma dwa kąty równe ⇒ jest równoramienny
no więc tak
|∡ABC|=α
wtedy |∡BDF|=90o−α ponieważ w trójkącie kąty sumują się do 180o
|∡ACB|=180o−2α również z tego powodu
|∡DCE|=2α tego chyba nie muszę tłumaczyć
|∡DEC|=90o−α również z powodu kątów w trójkącie
ma dwa kąty równe ⇒ jest równoramienny