Nierówność Pati: Dwusieczna kąta zewnętrznego przy wierzchołku C trójkąta ABC przecina prostą AB w punkcie D. Niech |AC|=b, |BC|=a, |CD|=d i b>a. Wykaż, że d< ^2ab_b−a

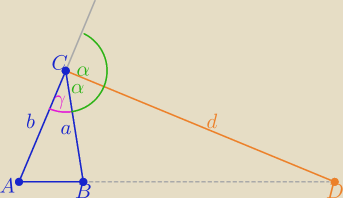
Eta: 1/ rysunek 2/ γ= 180^o−2α ⇒ sinγ= sin2α = 2sinα*cosα , α∊(0,90^o) to cosα∊(0,1) 3/ γ+α= 180^o−α ⇒ sin(γ+α)=sinα 4/ b>a P(ΔACD)=P(ΔABC)+P(ΔBCD)

1		1		1
	*bd*sin(γ+α)=		ba*sinγ+		ad*sinα
2		2		2

bdsinα=2absinαcosα+adsinα / :sinα≠0

	2ab
bd =2abcosα+ad ⇒ d(b−a)=2ab*cosα ⇒ d=		*cosα i cosα∊(0,1)
	b−a

	2ab
zatem d<
	b−a

============ c.n.w.