Geometria analityczna 365: Znaleźć równanie płaszczyzny przechodzącej przez dwa punkty M(2,−1,4) N(1,−1,5) i prostopadłej do płaszczyzny x − 2y + z − 1=0 Obliczylem wektor MN=[−1,0,1] i mam też wektor płaszczyzny n=[1,−2,1] Następnie mam obliczyć iloczyn tych dwóch wektorów? Proszę o pomoc

po prostu Michał: iloczyn wektorowy zrob. nastepnie podstaw do rownania plaszczyzny dowolny z punktow M lub N.

po prostu Michał: z iloczynu wektorowego pewnie otrzymasz cos w stylu [2,2,2] wiec nasze rownanie Ax + By + Cz + D = 0 po podstawie [2,2,2] i np. punktu M czyli (2,−1,4) D = ...

365: no tak mój wyszedł [2,0,2] D=−12 czyli rówanie płaszczyzny wygląda tak 2x−2z−12=0 Jaki będzie kolejny krok?

365: odp w ksiązce jest taka x+y+z−5=0

po prostu Michał: 1) policz jeszcze raz bo cos nie gra 2) skoro wyszlo Ci 2,0,2 to czemu przy "z" masz minus?

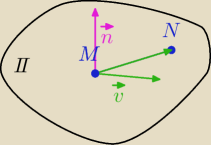
utem: π płaszczyzna przechodząca przez MN i prostopadła do płaszczyzny π₁: x−2y+z−1=0 v^→=[1,−2,1] wektor prostopadły do pł. π₁ v||π n^→=[−1,0,1] x [1,−2,1]=[2,2,2] || [1,1,1] π: 1*(x−2)+1*(y+1)+1*(z−4)=0 π: x+y+z−5=0

365: miales racje iloczyn wektorowy jest równy [2,2,2] D=−10 i teraz po podstawieniu i skróceniu wszstko się zgadza. Dziękuję