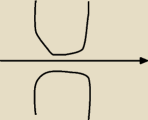
prosze o pomoc. Mateusz: Małe pytanko. Czy jeśli parabola znajduje się tak jak na rysunku nad osią X lub pod, ale jej nie dotyka , ani nie przecina to X€ do zbioru pustego? I pytanie nr 2 (x−3)² ≥)0 X0=3 Parabola styka się swoim wierzchołkiem z punktem 3 na osi x, i teraz pytanie , jak mam to poprawnie zapisać? X∊R \{3} − X należy do liczb rzeczywistych poza 3 czy X∊{3} Bardzo dziękuję za ewentualne odpowiedzi.

Jolanta: x∊R

Mateusz: @Jolanta chodzi Ci tutaj o moje pierwsze pytanie tak?

Jolanta: Tak

po prostu Michał: jesli piszesz x ∊ ... to masz na mysli dziedzine, a dziedzina paraboli to zbior liczb rzeczywistych. Prawdopodobnie masz na mysli przyklad, ze kiedy np. nierownosc jest spelniona przez zbior liczb rzeczywistych, to wtedy tak, parabola jest nad osia, jesli nierownosc jest ostra (<, >) lub dotyka w jednym miejscu os OX (nierownosc nieostra ≤ , ≥) Zatem do pytania nr 2 (x−3)² ≥ 0 to ta nierownosc jest spelniona dla wszystkich liczb rzeczywistych, nawet dla x=3 gdyz (3−3)² = 0 ² = 0 , a 0 ≥ 0.

Jolanta: Ale w 2) także

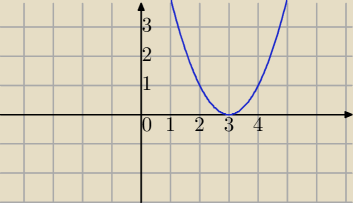
Mila: To zależy od pytania. 1) (x−3)² ≥0 dla x∊R 2) (x−3)²≤0 dla x=3 3) (x−3)²<0 brak rozwiązań ( niektórzy piszą x∊∅, ale to wg mnie błędny zapis, bo jak może coś należeć do zbioru pustego) 4) (x−3)²>0 x∊R\{0} albo zapis: x∊(−∞,3)∪(3,∞)

Mateusz: Czyli jak podpiszę rysunek w takim przykładzie X∊R , to nauczyciel nie powinien się do niczego przyczepić , tak?

Jolanta:

Mateusz: Dziękuję wszystkim , za odpowiedzi. Pozdrawiam

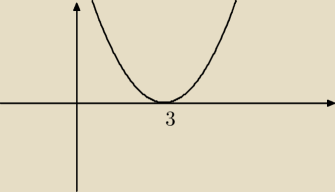
Jolanta: W tym przypadku (x−3)² ≥0 czyli y≥0 dla x ∊R

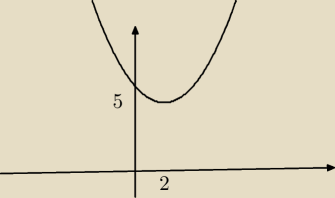
Mateusz: Jeszcze jedno , sorka , że zawracam głowę. Jeśli jest przykład : −5≥(x−2)² to piszę , że brak rozwiązania i tyle tak? Jak wyglądałby ewentualny rysunek do tego przykładu?

Jolanta:

Jolanta: Brak rozwiazan ponieważ nie ma y ≤0

Mateusz: @Jolanta, dziękuję

Jolanta: A jeśli chodzi o zapis −5≥ (x−2)2 0≥ (x−2)²+5

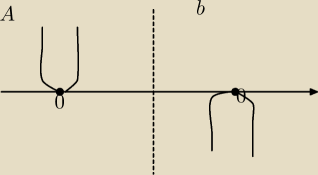
Mateusz: A czy mogłabyś Mi pomóc jeszcze w tym ? W sensie , czy dobrze robie: A)x²≥0 x∊R Parabola w skierowana w górę. B)x²≤0 x∊R parabola skierowana w dół −x²≥0 i tutaj nie wiem

po prostu Michał: skoro x² to parabola skierowana w gore skoro −x² to w dół.

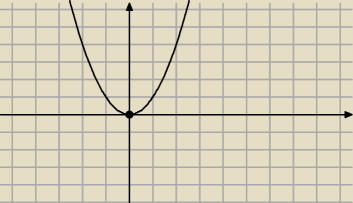
AiO: B −zle x²≤0 dla x=0

po prostu Michał: A) x² ≥ 0 −−> parabola skierowana w gore, x ∊ R B) x² ≤ 0 −−> parabola skierowana w gore, jedyna liczba spelniajaca nierownosc to x=0 (bo patrzymy ponizej osi OX bo ≤ 0) C) −x² ≥ 0 −−> parabola skierowana w dół, patrzymy kiedy jest powyzej osi OX (bo ≥ 0) i sie zgadza tylko dla x=0

Jolanta: o tym jak parbola ma ramiona decyduje znak przed x² y=−3x² w dól y=5x² w góre

Jolanta: Moze Ci sie przyda parabola moze byc przesunieta w bok ale takze w góre i w dól postac kanoniczna pokazuje nam te przesuniecia y=a(x−p)²+q p=x_w q=y_w y=2(x−3)²−5 parabola y=2x² ma wierzchołek W(3,−5) czyli została przesunieta o 3 jednostki w prawo i 5 w dół