:( halo: Pole powierzchni bocznej ostrosłupa prawidłowego czworokątnego jest 2 razy większe od pola jego podstawy. Oblicz kosinus kąta nachylenia krawędzi bocznej do płaszczyzny podstawy ostrosłupa. Obliczyłam, że h=a Niestety nie wiem co dalej

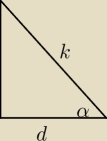
Jerzy: Najpierw oblicz krawędź k. Potem z rysunku oblicz cosα. d − połowa przekatnej podstawy

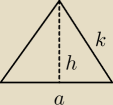
Jerzy: To rysunek do policzenia krawędzi k.

halo: Nie wiem jak to zrobić

Jerzy: k − policz z tw. Pitagorasa.

halo: Wiem, że z pitagorasa ale nadal nie umiem

Jerzy:

	a		h
h2 + (		)2 = k ⇔ h2 + (		)2 = k ... i oblicz k.
	2		2

Jerzy: Oczywiście tam ma być: k²

halo: h²:2=k tak?

Jerzy:

	h2
Nie .... h2 +		= k2
	4

teraz licz k

halo: √5h:2=k²?

Jerzy: Przecież pierwiastkujesz obustronnie.

halo: No taaak. Dobra, jestem za głupia na takie zadania po prostu

Jerzy:

	√5
k =		*h
	2

...teraz licz cosα

halo: √2:√5?

Jerzy: Tak, tylko usuń niewymierność z mianownika.

halo: Okej, dziękuję