Wyznacz współrzędne punktu Q symetrycznego do punktu P K: Wyznacz współrzędne punktu Q symetrycznego do punktu P(−1, −4) względem prostej k: 5x+4y−20=0 Wyznaczyłem sobie to obrazowo w układzie współrzędnych i policzyłem paluchem, ale chciałbym znać sposób na przypadki gdy punkt będzie miał jakieś chore współrzędne, których nie da rady narysować

Mila: Piszę.

AiO: Nie rozumiem co to znaczy chore wspolrzedne i dlazcego nie darady narysowac ? czy liczby niewwymierne to sa chore liczby ? Jaki jest problem narysowac odcinek dlugosci √2 ? Przeciez to jest przekatna kwadratu o boku 1 . A √5 ? √2²+1² a√3 powiazany w wysokoscia w trojkacie rownobocznym . Wiec jakie chore?

Adamm: AiO, narysuj mi odcinek wielkości log₂3

Adamm: i pewnie chodziło o coś w stylu A=(1; 50) B=(2032; −40) C=(87; 52)

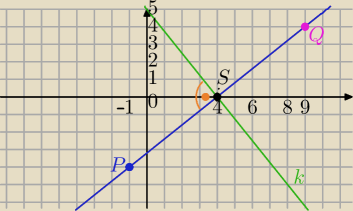
Mila: P(−1, −4) Q=(x,y) k: 5x+4y−20=0 1) piszemy równanie prostej prostopadłej do k i przechodzącej przez punkt P m⊥k m: 4x−5y+D=0 i 4*(−1)−5*(−4)+D=0⇔D=−16 m: 4x−5y−16=0 2) szukamy punktu przecięcia k i m 5x+4y−20=0 4x−5y−16=0 ===== x=4, y=0 S=(4,0) 3) P(−1, −4) ,Q=(x,y) Punkt S jest środkiem odcinka PQ⇔

	−1+x		−4+y
4=		i 0=
	2		2

x=9 i y=4⇔ Q=(9,4) ========= (Inaczej wsp. Q można wyznaczyc tak) PS^→=[5,4] S=(4,0)→T_[5,4]→Q=(4+5,0+4)=(9,4)

K: Miałem na myśli współrzędne typu A(789, −900)

AiO: . Nie ma chorych wspolrzednych i chorych liczb . Taki odcinek mozemy narysowac ale nie osiagniemy duzej dokladnosci rysujac na papierze milimetrowym starnny wykres funkcji y=2^x Odmierzamy na OY odcinek rowny 3 i prowadzimy przez otrzymany punkt rownolegla do OX az do punktu przeciecia z krzywa wykladnicza Bedzie on zawarty miedzy 1,5 i 1,6 . Mozna ?Mozna .

Adamm: wiesz, mówiąc narysuj, mam na myśli narysuj nie sobie przybliż

K: chorych rozumianych jako dobranych specjalnie przez nauczycielke tak, aby narysowanie ich sprawiło jak najwięcej problemów. Z góry postrzegane jako nieopłacalne do przedstawiania w układzie współrzędnych w porównaniu do metody algebraicznej. Najczęściej w takich sytuacjach prawdopodobieństwo popełnienia błędów rachunkowych jest o wiele wyższe i wolałbym znać oba sposoby, żeby nie być uzależnionym od jednego. Dziękuje #Milu za odpowiedź.

Adamm: K, jak przepiszesz z rysunku to pewnie ci obniży punkty tak czy siak

Mila: