Oblicz długości boków oraz miary kątów trójkąta ABC, jeśli: K: Oblicz długości boków oraz miary kątów trójkąta ABC, jeśli: A(√3, √3), B(3,√3), C(3+√3, 3+√3) |BA|=√(√3−3)²+(√3−√3)²=√3−6√3+9 |CA|=3√2 |CB|=2√3 z tw. cosinusów 12−6√3=18+12−6√6cosα −18−6√3=−6√6cosα nie wiem jak to dalej dokończyć, również mam problem z wyznaczaniem stopni z finalnej odpowiedzi. Proszę o pomoc.

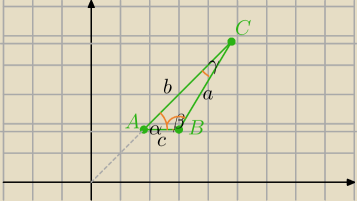
Mila: A(√3, √3), B(3,√3), C(3+√3,3+√3) 1) c=|AB|=√(3−√3)²+0²=3−√3 a=|BC|=√(3+√3−3)²+(3+√3−√3)²=√3+3²=√12=2√3 b=|AC|=√(3+√3−√3)²+(3+√3−√3)²=√3²+3²=3√2 2) c²=a²+b²−2a*bcos γ (3−√3)²=4*3+9*2−2*2√3*3√2 *cosγ 12−6√3=30−12√6cosγ −18−6√3=−12√6 cos γ

	18+6√3		3+√3
cosγ=		=
	12√6		2√6

	√6+√2
cosγ=
	4

γ=15^o 3) a²=b²+c²−2bc*cos α 4*3=9*2+12−6√3−2*3√2*(3−√3)*cosα 0=18−6√3−6*(3√2−√6) cosα −18+6√3=−6*(3√2−√6)*cosα/ : (−6) 3−√3=(3√2−√6)*cosα

	3−√3
cosα=		⇔
	3√2−√6

	√2
cosα=
	2

α=45^o β=180−(15+45)=120 ============== okazuje się, że może lepiej było liczyć b²=.. a²=..

K: γ=15^o to jest z tabeli wartości funkcji trygonometrycznych? bo cos dla 0,966 przyjmuje 75^o

Mila: Z tabeli wartości . wg wolfram http://www.wolframalpha.com/input/?i=arccos((sqrt(6)%2Bsqrt(2))%2F4) źle odczytałaś z tabeli

K: Okej, dziękuje za pomoc.

Mila: