Okresowosc AiO: Nastepna sprawa z ktora mam klopot To wyznaczanie okresy podstawowego funkcji trygonometrycznych Wiem ze pokresem podsatwowyn y=sinx i y=cos x jest 2π, i y=tgx i y=ctgx jest π Nie potrafie jednak to policzyc mam takie przyklady

	x
a) y=cos
	2

	x
b) y=tg
	3

	π
c) y=sin(x+		)
	2

d) y=|sinx| e)y= 1+2sinU{3}[2}x

	π
f) y=1−3sin(3x−		)
	4

co do c) to mysle ze mozna zapisac to tak y=cosx i T=2π reszte nie wiem

Mila: 1) f(x)=sin(a*x), g(x)=cos(ax) Okres:

	2π
T=		, a≠0
	a

2) f(x) =tg(ax), g(x)=ctg(ax)

	π
T=
	a

Licz teraz . Translacja nie ma wpływu na okresowość.

AiO: a) T= 2*π*2= 4π (ale czy tutaj nie bedzie 2π? b) T= 3π

	2		4
e) T= 2π*		=		π
	3		3

natomiast d i f) nie wiem jak zrobic

Mila: d) z wykresu f) a=3

	2π
T=
	3

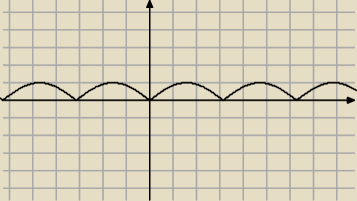
AiO: d) T=π co do f) to patrzymy tylko czy ax jest za funkcja ? Co do a ) to bedzie jednak 4 π Mila ktos kiedys pisal zeby wykorzystywac wzory na sume i roznice katow Mozesz cos wiecej na ten temat napisac ?Z gory dzieki .

Mila: Oczywiście . Ogólnie: f(x)=sin(ax), a≠0 Funkcja okresowa⇔ f(x)=f(x+T) , T niezależne od x sin(ax)=sin[a*(x+T)]⇔ sin(ax)−sin(ax+aT)=0

	ax+ax+aT		x−ax−aT
2*cos		*sin		=0
	2		2

	ax+ax+aT		−aT		aT
cos		=0 lub sin		=0⇔sin		=0
	2		2		2

T niezależne od x, zatem wyznaczamy z równości:

	aT		aT
sin		=0⇔		=kπ
	2		2

aT=2kπ

	2kπ
T=		okres zasadniczy:
	a

	2π
T=
	a

======

AiO: Piekne dzieki

Mila: