styczna Bidek: Znajdź równania stycznych do paraboli o równaniu y=x²−a gdzie a>0, w punktach przecięcia tej paraboli z osią OX, jeśli wiadomo, że styczne te są wzajemnie prostopadłe. ktoś napisał że :. Punkty przecięcia osi X przez parabolę leżą na tej osi, a styczne są prostopadłe względem siebie, stąd wiadomo że współczynniki kierunkowe prostych tych stycznych będą równe −1 i 1. no ale czemu −1 i 1 ? Przecież mogą mieć 4 i −1/4 ...

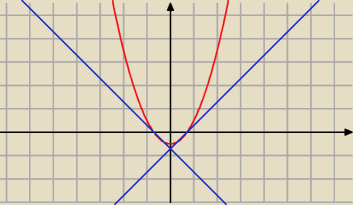
Janek191: y = x² − a , a > 0 0 = x² − a ⇒ x² = a x₁ = −√a x₂ = √a oraz y ' = 2 x a₁ = −2 √a a₂ = 2 √a y = −2 √a x + b₁ lub y =2 √a x + b₂ b₁ = 2 √2*(−√2) = − 4 b₂ = 4 zatem Odp. y = − 2 √a x − 4 lub y = 2√a x + 4 ============================================ Styczne mają być prostopadłe, więc −2 √a* 2√a = − 1 − 4 a = − 1

	1		1
a =		⇒ √a =
	4		2

	1
y = x2 −
	2

	√2		√2
x1 = −		x2 =
	2		2

	1
. y = − 2*		x + b1 = − x + b1 lub y = x + b2
	2

	√2		√2
b1 = −		b2 = −
	2		2

Odp.

	√2		√2
y = − x −		lub y = x −
	2		2

================================================

Janek191: Tam jest pomyłka − powinno być

	1
y = x2 −
	4

i wykonać potrzebne obliczenia