fs kot: Czy wysokosc trójkąta równoramiennego poprowadzona na podstawę zawsze pokrywa się z dwusieczną?

AiO: tak. Jest jednoczesnie dwusieczna i srodkowa

kot: A jak to udowodnić?

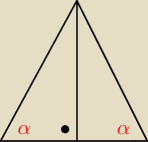
Adamm: szybki rachunek kątów

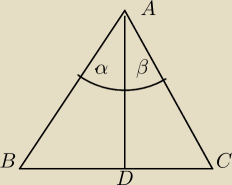
AiO: Tw W trojkacie rownoramiennym dusieczna kąta przy wierzcholku dzieli podstawe na polowy Zalozenie : w trojkacie ABC kat α= katowi β(czyli AD jest dwusieczna Teza: BD= DC czyli podsatwa podzielona na polowy Dowod : rozpatrzmy dwa trojkaty ADB i ADSC W tych trojkatach AB=AC jako ramiona trojkata rownoramiennego Bok AD wspolny kat α= katowi β zzalozenia wiec na podsatwie cech przystawania trojkatow BKB trojkatADB jest przystajcy do trojkata ADC Z rownosci tych trojkatow wynika tez rownosc odpowiednich elementow wiec BD=DC cnd Z rownosi tych trojkatow wynika tez ze kat B= katowi C Wniosek nr 1 W trojkacie rownoramiennym katy przy podsatwie sa rowne Z rownosci trojkatow ADB i ADC wynika dalej z kat ADB= katowi ADC ALe sa to katy przylegle wiec sa proste Stad mamy z eAD jest prostopadle do BC Wniosek nr 2 W trojkacie rownoramiennym dwusieczna kata przy wierzcholku jest prostopadla do podstawy .