Oblicz CD I DB
Uliczny Grajek:
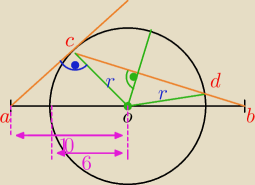
Środkiem O odcinka AB o długości 20 cm jest środek okręgu o promieniu 6 cm.
Przez punkt A poprowadzono styczną do okręgu w punkcie C. Odcinek CB przecina okrąg
w punkcie D. Oblicz |CD| i |DB|.
|DB| * |CB| = (|OB| − r) * (|AO| + r)
|DB| * |CB| = 4 * 6
|DB| * |CB| = 64
21 maj 13:18
Quadrat: 2 linijka 4 * 16
Ktoś ma jakieś pomysły?
21 maj 14:01
an: pole Δ ABC wysokość CE i dalej AE, EB , BC⇒DB i CD
21 maj 14:11
Quadrat: Jak mam znaleźć wysokość CD?
21 maj 16:10
Quadrat: CE*
21 maj 16:16
squirel: moze sprubuj z pitagorasa to obl
21 maj 19:26
Quadrat: Co ty gadasz człowieku? Co mam niby obliczyć z pitagorasa?
*Spróbuj przez ó
21 maj 19:27
squirel: czm się bulwersujesz

? masz odc ac i oc . obl ao z pitagorasa i masz pr
21 maj 19:29
Quadrat : Dobra, dobra śmieszku. Wyjdź i nie zaśmiecaj forum
21 maj 19:30
squirel : KRETYNIE


! TŁUMACZE FIC ZE Z PITAGORASA OBL ODC

!
21 maj 19:35
Quadrat: Dlaczego mnie obrażasz i wprowadzasz w błąd? Proszę cię grzecznie byś opuścił mój wątek,
a najlepiej to forum, bo widocznie nie jest dla ciebie przeznaczone. Z całym szacunkiem lecz
jestem zmuszony do zakończenia tej dyskusji.
21 maj 19:38
Adamm: co prawda to co napisał squirel było niepotrzebne, ale faktycznie,
|BC| da się policzyć z tw. Pitagorasa
21 maj 19:59
Adamm: a to nie to co liczymy

21 maj 20:00
Adamm: no więc tak
najpierw z tw. Pitagorasa
r
2+(|AB|/2)
2=|AC|
2 ⇒ |AC|=...
dalej
wysokość ACO padająca na przeciwprostokątną wynosi h=...
teraz niech spodek tej wysokości to S
h
2+|SA|
2=|AC|
2 ⇒ |SA|=...
dalej
|AB|=|SA|+|SB| ⇒ |SB|=...
|SB|
2+h
2=|CB|
2 ⇒ |CB|=...
no ostatecznie, z twierdzenia o stycznej i siecznej
|AC|
2=|CB|*|BD| ⇒ |BD|=...
|BD|+|DC|=|CB| ⇒ |CD|=...
i zadanie rozwiązane

21 maj 20:05
Mila:
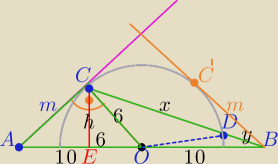
1)
W ΔACO: m
2=10
2−6
2,⇔m=8
P
ΔACO=24
2)
W ΔCEO:
|EO|
2+4.8
2=6
2
|EO|=3.6
3) W ΔCEB:
|CB|
2=h
2+(|EB|)
2
|CB|
2=4.8
2+(3.6+10)
2
|CB|
2=208
|CB|=
√208=4
√13
4)
8
2=y*(x+y)
64=y*4
√13
16=y*
√13
| | 16 | | 36√13 | |
|CD|=4√13− |
| √13= |
| |
| | 13 | | 13 | |
Zgadza się z odpowiedzią?
21 maj 21:14
Quadrat: Zgadza się

Dziękuję wszystkim wam za pomoc

21 maj 21:19
 Środkiem O odcinka AB o długości 20 cm jest środek okręgu o promieniu 6 cm.
Przez punkt A poprowadzono styczną do okręgu w punkcie C. Odcinek CB przecina okrąg
w punkcie D. Oblicz |CD| i |DB|.
|DB| * |CB| = (|OB| − r) * (|AO| + r)
|DB| * |CB| = 4 * 6
|DB| * |CB| = 64
Środkiem O odcinka AB o długości 20 cm jest środek okręgu o promieniu 6 cm.
Przez punkt A poprowadzono styczną do okręgu w punkcie C. Odcinek CB przecina okrąg
w punkcie D. Oblicz |CD| i |DB|.
|DB| * |CB| = (|OB| − r) * (|AO| + r)
|DB| * |CB| = 4 * 6
|DB| * |CB| = 64
 ? masz odc ac i oc . obl ao z pitagorasa i masz pr
? masz odc ac i oc . obl ao z pitagorasa i masz pr

 ! TŁUMACZE FIC ZE Z PITAGORASA OBL ODC
! TŁUMACZE FIC ZE Z PITAGORASA OBL ODC  !
!


 1)
W ΔACO: m2=102−62,⇔m=8
PΔACO=24
1)
W ΔACO: m2=102−62,⇔m=8
PΔACO=24
 Dziękuję wszystkim wam za pomoc
Dziękuję wszystkim wam za pomoc 