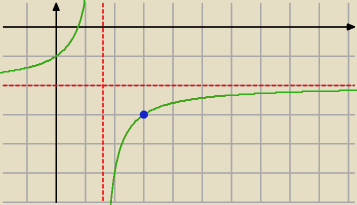
funkcja homograficzna Jokerkaa: Na rysunku przedstawiony jest fragment wykresu funkcji homograficznej F określonej

	m
wzorem F(x)=		+ {b} , gdzie m≠0 i x≠a . Ponadto wiadomo, że do wykresu
	x−a

funkcji F należy punkt A(4, −6) [niebieska kropka na rysunku] a) napisz wzór funcji F w postaci ilorazu dwóch wielomianów pierwszego stopnia. b) sprawdź, czy punkt B( 1−√2 , −2 −√2 ) należy do wykresu funkcji F. c) nie wykonując obliczeń ustal znak liczby |F(−π)| + F(π). uzasadnij odpowiedź. d) rozwiąż równanie F(x)= −2x + 2.

kochanus_niepospolitus: 1) wiesz gdzie masz asymptotę pionową (o wzorze x=a) ... to jest właśnie to 'a' ze wzoru funkcji 2) wiesz, że asymptota poziom wynosi y=2 ... stąd lim_{x−>+/−∞} F(x) = 2 −> b = 2 3) podstawiasz pod wzór funkcji współrzędne punktu A i wyliczasz 'm'.