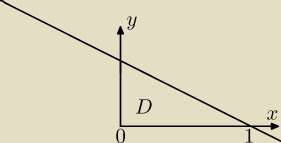
Całka podwójna ograniczona prostą i osiami współrzędnych Darkoozz: Hej, chciałbym prosić o pomoc w znalezieniu błędu w moich obliczeniach. Mam takie zadanie: Obliczyć całke podwójna ∫∫(5x²−2xy)dxdy w trójkącie ograniczonym prostą x+2y=2 i osiami współrzędnych Obszar który całkuje: 0≤x≤1 0≤y≤−1/2x+1 ∫(5x²−2xy)dy = 5x²y−xy² Z oznaczonej wyszło mi −11/4x³+6x²−x Potem nieoznaczona ∫(11/4x³+6x²−x)dx =−11/16*x⁴+2x³−1/2x² I oznaczona wychodzi mi 13/16 a powinno być 3. Sprawdzałem obliczenia na kalkulatorach online i niby są dobrze, czyżby błąd tkwił w obszarze całkowania? =−

'Leszek: obszar całkowania D: 0 ≤ x ≤ 2 , 0 ≤ y ≤ (−1/2)x +1

Darkoozz: No tak nie wiem czemu odrazu tego nie sprawdziłem, dziekuje