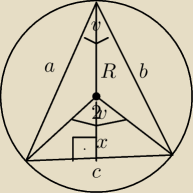
Ekstrema funkcji wielu zmiennych- optymalizacja Kabuuz: Mam takie zadanie Wśród trójkątów wpisanych w koło o promieniu R znaleźć ten, który ma największe pole. Zrobiłem taki rysunek.

1
	*(R+x)*c=S
2

a²+b²−abcos(v)=c² 2R²−cos(2v)=c² S=√p*(p−a)(p−b)(p−c) x=Rcos(v) Z tych równań wychodzę na wielkiego tasiemca tylko z niewiadomymi a, b, c tylko czy dobrze się za to zabrałem? Można to jakoś łatwiej zrobić bo jakoś nie widzi mi się wymnażanie tego bo to zajmuje 2 linijki drobnym druczkiem zeszytu A4?

Kabuuz: S to pole trójkąta

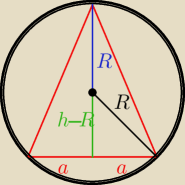
po prostu Michał: Niech podstawa ma dlugosc 2a (dla prostszych obliczen) z Pitagorasa R² = (h−R)² + a² no to wlasciwie wszystko co trzeba wiedziec.

	1
PΔ =		* (2a) * h = a*h
	2

z tego tam wzoru wyzej (z tym R) wyznacz albo "a" albo "h" i tutaj podstaw potem pochodna i inna zabawa PS −> tak, wziales sie za to zadanie w bardzo nieprzyjemny sposob

Adamm: po prostu Michał, to nie jest trójkąt równoramienny

	abc
P=		i tw. Sinusów
	4R

masz funkcję dwóch zmiennych, odpowiednia dziedzina, jest do policzenia

po prostu Michał: aj, faktycznie, nie doczytalem ze nie musi byc rownoramienny.

Kabuuz:

	ab√3
Wyszło mi takie coś f(a,b)=		c=R√3
	4

Tylko co teraz. Łatwo zauważyć że żeby pole było największe to a musi być takie samo jak b ale można to jakoś rozpisać?

Kabuuz: ?

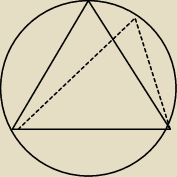
jc: Przecież widać, że równoramienny, ale dlaczego równoboczny? (dla ustalonej podstaw, równoramienny ma jest najwyższy, więc ma największe pole)

Kabuuz: Napisałem zadanie a wszyscy patrzą na ten rysunek. Napisałem że ja go zrobiłem ale on służył mi tylko do celów poglądowych. Zadanie tyczy się dowolnego trójkąta wpisanego w koło o promieniu R tak jak jest to wcześniej napisane

jc: Dowolny trójkąt ≤ trójkąt równoramienny o tej samej podstawie ≤ trójką równoboczny Wystarczy zająć się drugą nierównością.

jc:

	R2
Pole =		(sin 2α + sin 2β + sin 2γ) (dlaczego?)
	4

α+β+γ = π, α, β, γ > 0 Możemy założyć, że α, β, γ ≤ π/2 (dlaczego?). Dla takich kątów funkcja sin 2α jest wypukła. (sin 2α + sin 2β + sin 2γ)/3 ≤ sin 2(α+β+γ)/3 = sin 2π/3 = √3/2 "=" mamy tylko dla równych kątów

	3√3
Wtedy Pole =		R2.
	8

Sprawdź, bo mogłem coś pomylić. Dowód rozszerza się na n−kąt wypukły wpisany w okrąg.