Szkicowanie funkcji trygonometrycznej K: Czy ktoś mógłby mi przedstawić krok po kroku rysowanie funkcji: f(x)=sin²x+|cosx|*cosx ∊<−2π,2π> Wykres finalnie powinien wyglądać tak: http://i.imgur.com/fZzDmA4.png Proszę o pomoc : (

K: Ktokolwiek? : /

Adamm: jeśli cosx<0 to funkcja wygląda tak f(x)=sin²x−cos²x=−(cos²x−sin²x)=−cos2x co jeśli cosx≥0 ?

mat: cosx≥0, to f(x)=1 cosx<0, to f(x)=−cos2x

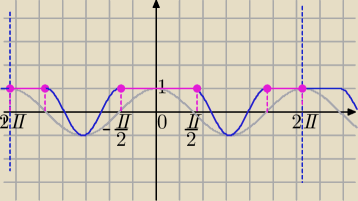
Mila: f(x)=sin²x+|cosx|*cosx , x∊<−2π,2π>

	3π		π		π		3π
1) |cosx| =cosx dla cosx≥0⇔ x∊<−2π, −		>∪<−		,		>∪<		,2π>
	2		2		2		2

(najlepiej naszkicować wykres funkcji y=cosx) wtedy f(x)=sin^x+cos²x=1 2) |cosx|=−cosx dla cosx<0 wtedy f(x)=sin²x−cos²x=−(cos²x−sin²x)=−cos(2x)

K: Dobra wszystko już jasne, dziękuje za pomoc.

Mila: