Diagramy
nocnaćma:
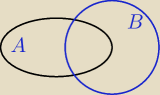
Na diagramie zbiorow A i B zanacz czesc pusta w przypadku gdy :
a) A−B=A
b) A⊂B
c)A=B
d)AUB=A∩B
e)A∩B=∅
f)A∩B=A
g)AUB=B
h) B−A=B
i)A−B=∅
j)(AUB)−B=A
k) A−B=B−A
Mam pytanie . Jak to rysowac ?
18 maj 09:03
zegarmistrz:
Idź do grafika komputerowego, to ci pokaże.
18 maj 09:03
nocnaćma: Wlasnie tak zrobie jak piszesz .
Dzieki serdeczne za dobra rade

18 maj 09:15
nocnaćma:

Chyba juz powoli łapię
np A∩B=A
A∩B to kreski czarne
A∩B=A to obszar czerwony ktory nalezy do A
18 maj 10:20
powrócony z otchłani:
Czerwone kreski = ten obszar jest pusty

Jezeli tak to dobrze.
18 maj 10:32
nocnaćma: Witaj

tak jak napisales
18 maj 10:33
powrócony z otchłani:
Jak bede przed kompem to bede mogl Ci pomoc z diagramami Venne'a. Obecnie komorkowy jestem wiec
mam mocno ograniczone mozliwosci
18 maj 10:37
nocnaćma: Dobrze . dzieki
18 maj 10:42
kochanus_niepospolitus:
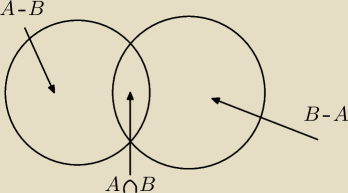
No to lecimy po kolei:
a) A−B=A ⇔ A∩B=∅ (bo tylko wtedy zbiór B przy odejmowaniu 'nic nie zje' ) czyli są
rozdzielne
b) A⊂B ⇔ A−B=∅ (bo zbiór A w całości jest wewnątrz zbioru B)
c)A=B ⇔ B−A=∅ i A−B=∅ (skoro są równe to nic nie 'wystaje' poza te zbiory)
d)AUB=A∩B ⇔ A=B (tylko wtedy suma równa się części wspólnej), więc patrz wyżej
e)A∩B=∅ ⇔ patrz punkt (a)
f)A∩B=A ⇔ Czyli A−B=∅ (czyli mamy A zawarty w B ... patrz (b) )
g)AUB=B ⇔ Znowu mamy A−B=∅ (czyli mamy A zawarty w B ... patrz (b) )
h) B−A=B ⇔ poprzez analogię do punktu (a)
i)A−B=∅ ⇔ Czyli A jest zawarte w B (patrz punkt (b))
j)(AUB)−B=A ⇔ A∩B=∅ (patrz punkt (a) )
k) A−B=B−A ⇔ A−(A∩B) = B − (A∩B) ⇔ A = B (patrz punkt (c) )
18 maj 11:59
nocnaćma: dzieki za trud

18 maj 12:05
kochanus_niepospolitus:
Najistotniejsze w diagramie Venne'a i tego typu zadaniach jest:
1) Wkucie sobie powyższego rysunku i zapamiętanie co oznaczają poszczególne części
2) Przeanalizowanie równości i wyznaczenie co musi być częścią pustą (z tych trzech rzeczy
które masz do wyboru) aby zachodziła równość
18 maj 12:08
 Na diagramie zbiorow A i B zanacz czesc pusta w przypadku gdy :
a) A−B=A
b) A⊂B
c)A=B
d)AUB=A∩B
e)A∩B=∅
f)A∩B=A
g)AUB=B
h) B−A=B
i)A−B=∅
j)(AUB)−B=A
k) A−B=B−A
Mam pytanie . Jak to rysowac ?
Na diagramie zbiorow A i B zanacz czesc pusta w przypadku gdy :
a) A−B=A
b) A⊂B
c)A=B
d)AUB=A∩B
e)A∩B=∅
f)A∩B=A
g)AUB=B
h) B−A=B
i)A−B=∅
j)(AUB)−B=A
k) A−B=B−A
Mam pytanie . Jak to rysowac ?

 Chyba juz powoli łapię
np A∩B=A
A∩B to kreski czarne
A∩B=A to obszar czerwony ktory nalezy do A
Chyba juz powoli łapię
np A∩B=A
A∩B to kreski czarne
A∩B=A to obszar czerwony ktory nalezy do A
 Jezeli tak to dobrze.
Jezeli tak to dobrze.
 tak jak napisales
tak jak napisales
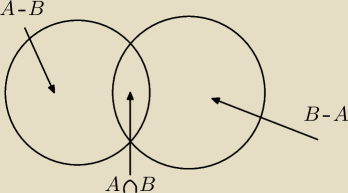 No to lecimy po kolei:
a) A−B=A ⇔ A∩B=∅ (bo tylko wtedy zbiór B przy odejmowaniu 'nic nie zje' ) czyli są
rozdzielne
b) A⊂B ⇔ A−B=∅ (bo zbiór A w całości jest wewnątrz zbioru B)
c)A=B ⇔ B−A=∅ i A−B=∅ (skoro są równe to nic nie 'wystaje' poza te zbiory)
d)AUB=A∩B ⇔ A=B (tylko wtedy suma równa się części wspólnej), więc patrz wyżej
e)A∩B=∅ ⇔ patrz punkt (a)
f)A∩B=A ⇔ Czyli A−B=∅ (czyli mamy A zawarty w B ... patrz (b) )
g)AUB=B ⇔ Znowu mamy A−B=∅ (czyli mamy A zawarty w B ... patrz (b) )
h) B−A=B ⇔ poprzez analogię do punktu (a)
i)A−B=∅ ⇔ Czyli A jest zawarte w B (patrz punkt (b))
j)(AUB)−B=A ⇔ A∩B=∅ (patrz punkt (a) )
k) A−B=B−A ⇔ A−(A∩B) = B − (A∩B) ⇔ A = B (patrz punkt (c) )
No to lecimy po kolei:
a) A−B=A ⇔ A∩B=∅ (bo tylko wtedy zbiór B przy odejmowaniu 'nic nie zje' ) czyli są
rozdzielne
b) A⊂B ⇔ A−B=∅ (bo zbiór A w całości jest wewnątrz zbioru B)
c)A=B ⇔ B−A=∅ i A−B=∅ (skoro są równe to nic nie 'wystaje' poza te zbiory)
d)AUB=A∩B ⇔ A=B (tylko wtedy suma równa się części wspólnej), więc patrz wyżej
e)A∩B=∅ ⇔ patrz punkt (a)
f)A∩B=A ⇔ Czyli A−B=∅ (czyli mamy A zawarty w B ... patrz (b) )
g)AUB=B ⇔ Znowu mamy A−B=∅ (czyli mamy A zawarty w B ... patrz (b) )
h) B−A=B ⇔ poprzez analogię do punktu (a)
i)A−B=∅ ⇔ Czyli A jest zawarte w B (patrz punkt (b))
j)(AUB)−B=A ⇔ A∩B=∅ (patrz punkt (a) )
k) A−B=B−A ⇔ A−(A∩B) = B − (A∩B) ⇔ A = B (patrz punkt (c) )
