asymtota oki: Skąd wiadomo kiedy wykrs funkcji przechodzi przez asymtopte poziomą?

Adamm: z rysunku

oki: ale wlasnie mam narysować rysunek i wyszła asymtota pozioma obustronna f(x)=x²/(x+2)²

kochanus_niepospolitus: o tym czy i jak funkcja 'przebija' asymptotę poziomą wyjdzie Ci gdy sprawdzisz monotoniczność funkcji oraz wyznaczysz wartości funkcji w ekstremach.

oki: a pionową tez może przeciąć?

piotr: asymptota pozioma y=1, równanie

x2
	= 1 ma rozwiązanie: x = −1
(x+2)2

a więc w tym punkcie wykres przecina swą asymptotę

piotr: pionowej nie może przeciąć, może co najwyżej jej "dotknąć"

Adamm: jeśli przez przeciąć masz na myśli, czy np. funkcja może mieć asymptotę x=a oraz wartość w tym punkcie, to tak, może

piotr: np funkcja f(x) = e^1/x ma asymptotę pionową x=0 prawostronną a z lewej strony zera mamy lim_x→0⁻ = 0, punkt (0, 0) nie należy do wykresu

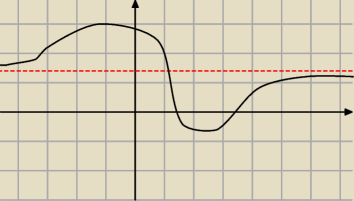
kochanus_niepospolitus: Może ilustracyjnie. Taka funkcja ma możliwość zaistnieć

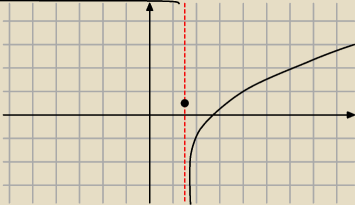
kochanus_niepospolitus: taka także

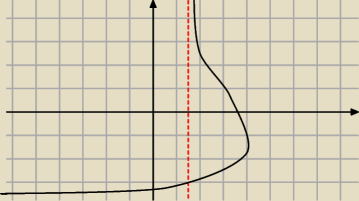
kochanus_niepospolitus: ale taka już nie ... bo to NIE JEST FUNKCJA

kochanus_niepospolitus: ponieważ dla tego samego 'x' (np. x = 2) funkcja przyjmuje dwie różne wartości

Adamm: kochanus, funkcja ℛ→ℛ to to nie jest, ale funkcja ℛ→ℛ² już tak