zbiór wartości kwiatuszek:

	7
wyznacz zbiór wartości funkcji f(x)=		bardzo proszę o pomoc ...
	sin2x−sinx−12

Adamm: sin²x−sinx−12≠0 Δ=49=7²

	1+7		1−7
sinx≠		oraz sinx≠
	2		2

sinx≠4 oraz sinx≠−3 dziedzina zatem to ℛ bo sinx przyjmuje wartości od −1 do 1

po prostu Michał:

	7
m =		/*sin2x−sinx−12
	sin2x−sinx−12

Δ ≥ 0 ... i na koniec założenie co do mianownika sin²x−sinx−12 ≠ 0 czyli policzyc to i podstawic do tej funkcji z "m" aby znalezc jakie nie pasuje

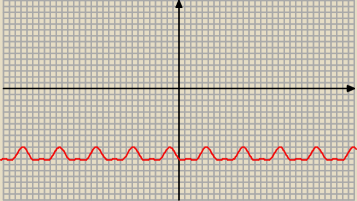
Adamm: tutaj masz rysunek funkcji w mianowniku teraz zauważyłem że przeczytałem dziedzina, ale robisz podobnie t=sinx

	7
g(t)=t2−t−12, f(g)=
	g

zbiór wartości t to <−1;1> zbiór wartości g to <−12,25;−10> zbiór wartości f to <−4/7;−7/10>

Adamm: pomyliłem się jeszcze, powinno być oczywiście zbiór wartości f to <−7/10; −4/7>

Adamm: robisz taki wężyk g(t) ma dziedzinę <−1;1> a zbiór wartości przyjmujesz jako dziedzinę f(g)

kwiatuszek: a czy mogę to zrobić w ten sposób : 1) t=sinx i t∊<−1,1> 2)sin²−sinx−12 =t²−t−12 i t∊<−1,1> ⇒ sin²−sinx−12 ∊<−12,25 , −10> (wyliczyłam jaki jest zbiór wartości t²−t−12 w przedziale od −1 do 1) 3) −12,25<sin²−sinx−12<−10

−1		1		−1
	>		>
12,5		sin2x−sinx−12		10

−4		7		−7
	>		>		czy takie rozwiązanie będzie poprawne?
7		sin2−sinx−12		10

Adamm: to prawie to samo co zrobiłem ja

kwiatuszek: tak, teraz widzę mam jednak wątpliwość co do przejścia z −12,25<sin2−sinx−12<−10 na ułamki...bo to jest podnoszenie obu stron nierówności do potęgi (−1)... i nie wiem czy można tak robić i ewentualnie jakie są zasady przy takim podnoszeniu(zmiana znaku itp.)...czy ktoś mógłby mi w tym pomóc?

Adamm: no właśnie, dlatego sposób pokazany w poście 16:04 jest bardziej uniwersalny nawet możesz sobie narysować

kwiatuszek: Bardzo dziękuję Adamm Twoje rozwiązanie faktycznie jest przystępne i chętnie będe z takiego sposobu korzystać...gdyby jednak ktoś wiedział jak jest z tym podnoszeniem do potęgi (−1) to byłabym wdzięczna za odpowiedź..chciałabym wiedzieć bo mogłoby mi się to przydać do innych zadań

Adamm: możesz zaznaczyć że sin²x−sinx−12<0 i rozpatrywać każdą nierówność z osobna