zadanka
as: majac dae rownanie okregu O:x2+y2+6x+9y−12=0 i rowanie prostej 2x+y=2 Oblicz dlugosc cieciwy
i zapisz rownanie jej symetralnej
dla jakich wartsci parametru k okregi przecinaja sie a dla jakiej sa styczne wew. jesli
r1=3k+2 r2=8 IS1S2I=I2k+20I
24 sty 20:09
as:
24 sty 20:36
ula:
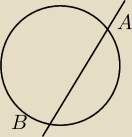
punkty A i B są wspólne okręgu i prostej więc rozwiąż układ równan
{x
2+y
2+6x+9y−12=0
{2x+y=2 →y=2−2x
po podstawieniu i wyliczeniu wyjdzie
x
2−4x+2=0
Δ=8
√Δ=2
√2
x
1=2+
√2 y
1=2−2(2+
√2)=−2−2
√2
x
2=2−
√2 y
2=2−2(2−
√2)=−2+2
√2
długość cięciwy to odległość między punktami AB
wzór
d=P{(x
A−x
B)
2+{y
A−y
B)
2} →tu jest pierwiastek na całej długości
podstaw
24 sty 21:08
ula: symetralna cięciwy
| | xA+xB | | yA+yB | |
wylicz najpierw środek odcinka BA z wzoru S=( |
| : |
| )
|
| | 2 | | 2 | |
oblicz potem kirunkową prostej przechodzącej przez p Ai B
kierunkowa szukanej prostej to
| | 1 | |
a2=− |
| (sa do siebie prostopadłe)
|
| | a1 | |
prosta y=a
2x+b która jest szukana symetralną) przechodzi przez punkt S czyli
y
S=a
2*x
S+b → wylicz b
podstaw do wzoru prostej
y=a
2x+b
24 sty 21:15
ak1: Czy dobrze napisałeś równanie okręgu i prostej ?
wychodzi mi że się nie przetną
24 sty 21:16
ak1: sorry, znalazłem swój błąd
24 sty 21:17
ula:
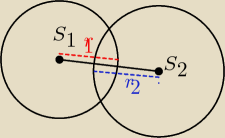
styczne to
IS
1S
2I=r
1+r
2 k=10
dwa punkty wspólne
Ir
1−r
2I<IS
1S
2I<Ir
1+r
2I
24 sty 21:24
ula: narysowałam rysunek z zalożeniem że jest ta cięciwa jeśli jej szukaja, nie narysowałam tego w
ukladzie równań
24 sty 21:26
ula: mam nadzieję, ze dalej sobie poradzisz

24 sty 21:27
as: heh dzieki bardzo
25 sty 07:02
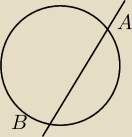 punkty A i B są wspólne okręgu i prostej więc rozwiąż układ równan
{x2+y2+6x+9y−12=0
{2x+y=2 →y=2−2x
po podstawieniu i wyliczeniu wyjdzie
x2−4x+2=0
Δ=8 √Δ=2√2
x1=2+√2 y1=2−2(2+√2)=−2−2√2
x2=2−√2 y2=2−2(2−√2)=−2+2√2
długość cięciwy to odległość między punktami AB
wzór
d=P{(xA−xB)2+{yA−yB)2} →tu jest pierwiastek na całej długości
podstaw
punkty A i B są wspólne okręgu i prostej więc rozwiąż układ równan
{x2+y2+6x+9y−12=0
{2x+y=2 →y=2−2x
po podstawieniu i wyliczeniu wyjdzie
x2−4x+2=0
Δ=8 √Δ=2√2
x1=2+√2 y1=2−2(2+√2)=−2−2√2
x2=2−√2 y2=2−2(2−√2)=−2+2√2
długość cięciwy to odległość między punktami AB
wzór
d=P{(xA−xB)2+{yA−yB)2} →tu jest pierwiastek na całej długości
podstaw
 styczne to
IS1S2I=r1+r2 k=10
dwa punkty wspólne
Ir1−r2I<IS1S2I<Ir1+r2I
styczne to
IS1S2I=r1+r2 k=10
dwa punkty wspólne
Ir1−r2I<IS1S2I<Ir1+r2I
