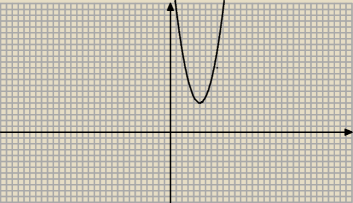
Prosta nierówność do udowodnienia misio: Prosta nierówność do udowodnienia x²y²+2x²+2y²−8xy+4>0 Czy można to udowodnić w ten sposób? x²(y²+2)−8xy+2y²+4>0 Δ=64y²−4(y²+2)(2y²+4)=64y²−8y⁴−32y²−32 Δ= −8(y⁴−4y²+4) ⇒ Δ<0 (rysunek) x∊R ⇒ y>0 ⇒ x²y²+2x²+2y²−8xy+4>0 c.n.w czy ten sposob jest poprawny?

Jerzy: A dlaczego Δ < 0 ?

jc: Wzór skróconego mnożenia. Δ = ...

piotr: dla y = −√2 i dla y = √2 Δ = 0

Jerzy: Dokładnie tak.

misio: mniejsza od zera ponieważ wyciągnałem −8 przed nawias, więc cokolwiek wstawię za y to bedzie Δ<0

Jerzy: Nawias za − 8 może przyjmować wartość 0.

piotr: czyli: dla x = −√2 ∧ y = −√2 oraz dla x = √2 ∧ y = √2 mamy niespełnioną nierówność.

misio: no tak oprócz √2 i − √2

jc: x²y²+2x²+2y²−8xy+4 = 2(x−y)² +(xy−2)² ≥ 0, dla x=y=√2 mamy zero, a więc nierówność jest słaba.

misio: dobra, jesli to jest zadanie za 3 punkty to ile bym za nie dostal?

piotr: Δ_y = 16−16 = 0

jc: 1 za próby rozwiązania?

Jerzy: Jeśli w treści jest nierówność słaba, to Twoje rozwiązanie będzie poprawne.

misio: a w poleceniu jest udowodnij dla dwóch różnych liczb x i y czy to cos nam zmieni?

Jerzy: Niestety nie.

jc: Jeśli x≠y, to mamy nierówność ostrą. Nadal 1 punkt za próby rozwiązania.