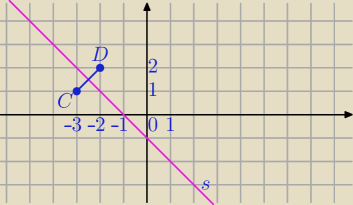
 1) Symetralna odcinka jest zbiorem wszystkich punktów płaszczyzny
jednakowo odległych od końców odcinka.
C= (−3;1) D= (−2;2)
P(x,y) ∊symetralnej CD⇔|PC|=|PD|⇔|PC|2=|PD|2
(x+3)2+(y−1)2=(x+2)2+(y−2)2
x2+6x+9+y2−2y+1=x2+4x+4+y2−4y+4
6x+9−2y+1=4x+4−4y+4⇔
2y=−2x−2
s: y=−x−1
−−−−−−−−−−
1) Symetralna odcinka jest zbiorem wszystkich punktów płaszczyzny
jednakowo odległych od końców odcinka.
C= (−3;1) D= (−2;2)
P(x,y) ∊symetralnej CD⇔|PC|=|PD|⇔|PC|2=|PD|2
(x+3)2+(y−1)2=(x+2)2+(y−2)2
x2+6x+9+y2−2y+1=x2+4x+4+y2−4y+4
6x+9−2y+1=4x+4−4y+4⇔
2y=−2x−2
s: y=−x−1
−−−−−−−−−−
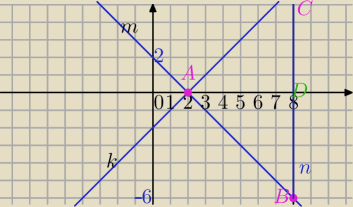 2)
x−y−2=0 , x+y−2=0 , x−8=0 ⇔
k: y=x−2
m: y=−x+2
n: x=8
a)
A=(2,0) punkt przecięcia prostych k i m
−x+2=x−2⇔−2x=−4, x=2 y=0
B: y=−x+2 i x=8 , y=−6
B=(8,−6)
C: y=x−2 i x=8
C=(8,6)
b) obwód:
Spróbuj sam
2)
x−y−2=0 , x+y−2=0 , x−8=0 ⇔
k: y=x−2
m: y=−x+2
n: x=8
a)
A=(2,0) punkt przecięcia prostych k i m
−x+2=x−2⇔−2x=−4, x=2 y=0
B: y=−x+2 i x=8 , y=−6
B=(8,−6)
C: y=x−2 i x=8
C=(8,6)
b) obwód:
Spróbuj sam
| 1 | ||
c) P= | *|BC|*|AD| | |
| 2 |