TRUDNE!! damian6699: Zadanie dla twardych Drut o długości 8m. podzielono na 2 części: z jednej zrobiono kwadratową ramkę a z drugiej ramkę w kształcie trójkąta równobocznego. Jak należy podzielić drut aby suma pól trójkąta i kwadrata była najmniejsza?

Anna: pomagam

damian6699: dobrze byłem z tym zadaniem na korkach i babka nie umiała mi tego rozwiązać..

Anna:

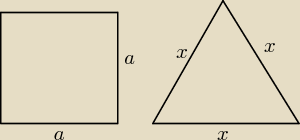
	8−3x
4x + 3x = 8 ⇒ 4a = 8−3x ⇒ a =
	4

	x2√3
f(a,x) = a2 +
	4

	8−3x		x2√3		64−48x+9x2+4x2√3
f(x) = (		)2 +		=		=
	4		4		16

	9+4√3
= x2*		− 3x + 4
	16

	b		3		8		24
xw= −		=		= 3*		=		=
	2a		9+4√3   2*   16		9+4√3		9+4√3

	24(9−4√3)		24(9−4√3)		8
=		=		=		(9−4√3)
	81−48		33		11

	8
Czyli bok trójkąta x =		(9−4√3), a na wykonanie trójkąta równobocznego zużyć należy
	11

	24
3*x =		(9−4√3) m
	11

	8−3x		3		3		8
Bok kwadratu a =		= 2 −		x = 2−		*		(9−4√3) =
	4		4		4		11

	6		54		24
= 2 −		(9−4√3) = 2 −		+		√3=
	11		11		11

	24		10
=		√3 − 2
	11		11

Na wykonanie kwadratu należy zużyć :

	24		32		96		128
4*a = 4*(		√3−		) = (		√3 −		) m
	11		11		11		11

Sprawdzenie:

	96		128		216		96		88
4a + 3x =		√3 −		+		−		√3 =		= 8 !
	11		11		11		11		11

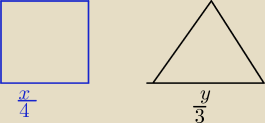Eta: Dla ułatwienia obliczeń

	x
oznaczamy dł. boku kwadratu przez
	4

	y
dł. boku trójkąta przez
	3

Ob kw. = x Ob tr. = y , x, y >0 to x+y= 8 => x = y−8 , dla y€(0,8)

	x
Pkw.= (		)2 = 116x2 = 116(y−8)2 = 4−y+116y2
	4

	1		y		y2
PΔ =		*(		)2*√3=		√3
	4		3		36

mamy zbadać minimum sumy pól: zatem: P= P_kw+P_Δ= 4 −4y +¹₁₆y² +¹₃₆√3y² to P(y) = ( ¹₁₆√3+¹₁₆)y² −y +4 −−− to funkcja kwadratowa , ramiona paraboli skierowane do góry więc osiąga minimum w wierzchołku dla odciętej:

	1		72
ymin=		*
	√3   1   2*( + )   16   16		72

	72		72( 9−4√3
ymin=		=		= 72( 9−4√3)
	9+4√3		(9+4√3)(9−4√3

to x _min = y−8 = 72( 9−4√3)−8 = 32(20−9√3) na takie dwie części należy rozciąć ten drut rachunki "koszmarne" ..... ale takie mają być PS. Myślę ,że te rachunki zniechęciły Twoją korepetytorkę do podania rozwiązania

damian6699: dziękuję

Eta: Mało,że rachunki koszmarne , to jeszcze pomyliłam się w przepisywaniu Anna ... wykonała je bezbłędnie w takim razie poprawię zapisy: P(y)= (¹₃₆√3+¹₁₆)y² −y +4

	1		1
ymin=		)=
	√3   1   2*( +   36   16		√3   1   + 18   8

	72
ymin=		....... po usunięciu niewymierności wynik powinienn zgadzać
	9+4√3

się z wynikami podanymi przez Anna jużz mi się nie bardzo chce dalej pisać

damian6699: to zadanie demotywuje

Eta: Tak , to prawda ...... jest w sam raz do "gnębienia " ucznia

Anna:

Eta: Przyznasz Anno ,że ciekawe jak ten drut w praktyce podzielić ? ( beznadzieja

Anna: Oczywiście! Czysta teoria, a dla ucznia − sadyzm!