Dla jakiej wartości parametru m równanie #62;'-')#62; #60;('-'#60;): Dla jakiej wartości parametru m równanie

	1
−		x4−(m2−m)x2−m4+1=0 ma cztery różne rozwiązania?
	4

Nie wychodzi mi coś : ( Δ₁>0 Δ₂>0 x₁≠x₂≠x₃≠x₄ x²=t t>0 −0,25t²−(m²−m)t−m⁴+1=0 Δ=m⁴−2m³+m²−m⁴+1=−2m³+m²+1 z hornera: (m−1)(−2m²−m−1)=0 Δ_m=−7 Nie wiem gdzie jest błąd, mógłby mi ktoś pomóc?

powrócony z otchłani: Nie masz bledu Zauwaz ze dla m<1 pierwszy nawias przyjmuje wartosc ujemna natomiast drugi nawias (jako ze a<0 oraz Δ<0 bedzie zawsze przyjmowal wartosci ujemne

#62;'-')#62; #60;('-'#60;): czyli tutaj nie może być czterech rozwiązań? bo jak może to nie wiem jak do tego teraz dojść...

Eta: "powrócony ... " zmień nick bo straszne źle na mnie działa ! !

Eta: https://pl.wikipedia.org/wiki/Otch%C5%82a%C5%84

#62;'-')#62; #60;('-'#60;): Czyli odpowiedź do tego zadania to m∊∅?

kochanus_niepospolitus: Etuś ... a czemuż to na Ciebie tak ten nick źle działa?

Eta: Życie jest piękne! a "otchłań"? brrrrrrrrrrrrrrrrrrrrrrrrrrrrrrrrrrrrrrrrrrrrrrrrrr

Eta:

kochanus_niepospolitus: ojjj ... a czyż ja nie właśnie nie powrócił z otchłani ... czeluści zła i występku

Eta:

#62;'-')#62; #60;('-'#60;): Zadania z wielomianów są potępiane przez społeczność tego forum czy jak?

Adamm: sekta wiecznej delty

Eta: #62 licz swoje zadania! Rysunki nie są dla Ciebie

#62;'-')#62; #60;('-'#60;): Bardziej chodzi mi o odpowiedź, bo nie jest to zadanie z podręcznika. Nie mam z czym porównać mojego końcowego wyniku.

kochanus_niepospolitus: #62 ... dla jakiego parametru 'm' równanie: Δ_t > 0 Masz już wyliczoną Δ_t tylko złe wnioski wyciągnięte zostały

#62;'-')#62; #60;('-'#60;): Δ_t>0 dla t∊(−1, 1)?

kochanus_niepospolitus: sprawdźmy: niech m=−100 Δ_t = −2*(−100)³ + (−100)² + 1 = 2*1'000'000 + 10'000 + 1 > 0

kochanus_niepospolitus: jak już wcześniej napisałem −−− źle wnioski wyciągnięte z etapu: Δ_t = (m−1)(−2m²−m−1)

#62;'-')#62; #60;('-'#60;): nie mam pojęcia jak to zrobić..............

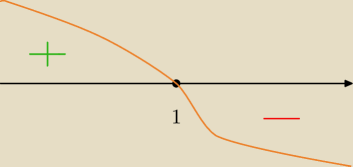
kochanus_niepospolitus: wyliczyłeś, że: (−2m²−m−1) = 0 Δ_m = −7 < 0 stąd wniosek: ∀_m∊R (−2m²−m−1) < 0 (bo a<0 i brak miejsc zerowych). więc szkic wykresu Δ_t wygląda następująco. Więc ... kiedy Δ_t > 0 dla jakich m

#62;'-')#62; #60;('-'#60;): No dla m∊(−∞, 1), patrze na wykres z geogebry i nie wiem jak do tego dojść. Jeżeli mam (m−1)(−2m²−m−1)>0 więc biore m>1 oraz Δ_m<0 więc m∊R, ale skąd się bierze to m<1 to już nie mam pojęcia. Nie wiem gdzie robie ten durny błąd ale strasznie mnie to irytuje, że tego nie widzę.

kochanus_niepospolitus: po pierwsze ... WYCIĄGNIJ (−2) z drugiego nawiasu po drugie ... wtedy drugi nawias jest ZAWSZE DODATNI po trzecie ... o znaku całego wyrażenia mówi współczynnik 'a' (czyli −2) oraz pierwszy nawias i stąd wiesz Chciałbym zasugerować, że metoda 'wężyka' to poziom (mniej więcej) gimnazjum.

#62;'-')#62; #60;('-'#60;): aha czyli mógłbym sobie rozumować to tak: że jedynym miejscem zerowym jest liczba 1, współczynnik przy najwyższej potędze jest ujemny więc zaczynamy rysować od dołu i wychodzi nam to: http://i.imgur.com/5GDrbAT.png

#62;'-')#62; #60;('-'#60;):

⎧	Δ>0
⎨	t1t2>0
⎩	t1+t2>0

1) (m−1)(−2m²−m−1)=0 m∊R/{1} 2) 1−m⁴>0 m∊(−1, 1) 3) m²−m>0 m∊(−∞, 0) U (1, +∞) Odp: m∊(−1, 0) Aby były cztery rozwiązania muszą wyjść dwa pierwiastki t₁>0 oraz t₂>0 więc nie rozumiem dlaczego wynik się nie zgadza z tymi założeniami co wypisałem.