kombinatoryka
Adamm: mamy n−kąt foremny (n≥3)
wybierając 3 wierzchołki, jakie jest prawd. że utworzą one trójkąt ostrokątny
zadanie wymyślone, jeśli ktoś rozwiąże, to dajcie znać o trudności tego zadania
15 maj 13:00
Adamm: a jakie prawd. byłoby gdybyśmy wybierali 3 punkty na okręgu?
15 maj 13:06
kochanus_niepospolitus:
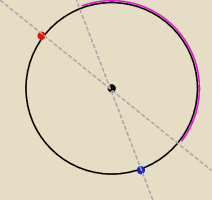
Jeśli chodzi o okrąg to sprawa prosta:
wybieramy kolejno wierzchołka A, B, C
A −−− dowolnie
B −−− dowolnie
C −−− na fioletowej części okręgu (uzależniona jest od pozycji B względem A i środka okręgu)
z wielokątami to musiałbym bawić się w indukcję, a szczerze mówiąc ... nie chce mi się tego
robić

15 maj 13:25
Adamm: kochanus, nie wiedziałem że można tak mnożyć, to co napisałeś ma sens, dzięki
15 maj 13:32
Adamm: w sumie to wiedziałem, ale tutaj mamy długość, a zazwyczaj jest pole czy objętość
15 maj 13:35
kochanus_niepospolitus:
wpisuję po prostu długość 'linii' na jaką 'rzucamy' punkty A,B,C
| | 1 | |
Jedyne czego ktoś może nie wiedzieć, to dlaczego przyjmuję, że punkt C leży w |
| części |
| | 4 | |
okręgu (szczerze mówiąc, to nie wiem czy na poziomie liceum można to wyjaśnić

)
15 maj 13:39
Adamm: punkt C rozumiem na zasadzie intuicji, fioletowy obszar uśrednia się do 1/4 okręgu
w sumie to chyba można to też obliczyć za pomocą całki
15 maj 13:43
g:
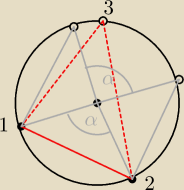
Wersja z okręgiem
Załóżmy że wybieramy punkty po kolei. Funkcja gęstości prawdopodobieństwa kąta między
pierwszym a drugim punktem jest stała i równa f(α) = 1/π. Trójkąt będzie ostrokątny jeśli
trzeci punkt znajdzie się na łuku o rozpiętości kątowej α, czyli z prawdopodobieństwem
warunkowym równym α/2π (warunkiem jest że kąt jest równy α).
Szukane prawdopodobieństwo to prawdopodobieństwo całkowite
| | α | | 1 | | 1 | | π2 | | 1 | |
P = ∫0π f(α)* |
| dα = |
| ∫0π αdα = |
| * |
| = |
| |
| | 2π | | 2π2 | | 2π2 | | 2 | | 4 | |
15 maj 13:44
Adamm: nie mówiłem o czymś takim, tylko o prawd. geometrycznym, bo tego już w ogóle nie rozumiem
15 maj 13:56
'Leszek: Dla ucznia ze szkoly sredniej wedlug mnie wystarczy pokazac to na rysunku ,ktory
przedstawil @ g: aby spelniony byl warunek zadania , trojkat ostrokatny to p.3 moze
znajdowac sie tylko na luku cwiartki okregu .Jest to oczywiscie wizualizacja zadania, ale
bardzo pogladowa i zrozumiala .
15 maj 14:11
Rafal: Czy mógłby mi ktoś wyjaśnić, dlaczego fioletowy łuk ma długość 2πr/4?
15 maj 18:30
Adamm: Rafal, fioletowy łuk nie ma długości 2πr/4
15 maj 18:34
Rafal: Właśnie dlatego pytam, zauważyłem teraz rozwiązanie g, więc już nie ważne.
15 maj 18:39
kochanus_niepospolitus:
Postaram się to wyjaśnić 'na chłopski rozum', ale to chwilkę zajmie

15 maj 18:56
kochanus_niepospolitus:
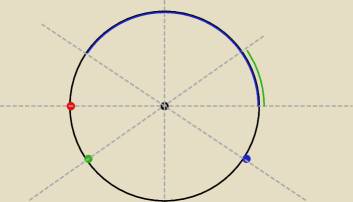
Punkt 'A' jest wybierany losowo, ale że mamy okrąg to jakbyśmy nie wybrali punkt
A, tak
możemy tak przekręcić kartkę aby znalazł się w 'lewym rogu' (nie czepiać się

).
Podzielmy teraz okrąg na 4 ćwiartki.
Zauważ, że dla każdego (dowolnie wybranego) punktu
B istnieje jego odpowiednik
B'.
Suma tych długości tych dwóch łuków
niebieskiego i
zielonego zawsze będzie równa
połowie obwodu okręgu (πr).
Im bliżej
B będzie 'dolnej części okręgu' tym mniejszy będzie ten łuk (i dążył do
| | πr | | πr | |
|
| ) a jednocześnie zielony łuk będzie większy (i także dążył do |
| ) |
| | 2 | | 2 | |
I tutaj musisz na intuicję (najłatwiej) zauważyć, że ŚREDNIA długość tego łuku będzie równa
| | πr | |
1/4 obwodu okręgu czyli właśnie |
| . |
| | 2 | |
Mam nadzieję, że w miarę rozumiesz.
A tak żeby Ci zagmatwać trochę sprawę to napiszę tylko, że z prawdopodobieństwem równym 1 mogę
| | πr | |
napisać, że ten łuk NIGDY nie będzie miał długości DOKŁADNIE |
| (tak samo jak z pr. |
| | 2 | |
równym 1 punkt B nie będzie leżał na prostej przechodzącej przez środek okręgu i punkt A).
15 maj 19:06
kochanus_niepospolitus:
Jedyne co jeszcze musisz zrozumieć, to to dlaczego ten trzeci punkt musi leżeć gdzieś na tym
łuku.
Jako wskazówkę proponuję Ci zajrzeć do tw. o kątach opartych na tym samym łuku oraz kącie
środkowym.
15 maj 19:08
Adamm: kochanus, myślę że Rafal jest świadom czemu musi tam się znajdywać
w końcu interesuje się geometrią
15 maj 19:09
Rafal: kochanus, dziękuję, oczywiście samą ideę "uśredniania" rozumiem, ale jednak długość tego
łuku zależy od położenia punktu B. Widocznie muszę się bardziej zagłębić w prawdopodobieństwo
na poziome akademickim.
15 maj 19:29
kochanus_niepospolitus:
Rafał ... na poziomie akademickim jest bardzo często takie zadanie:
na odcinku [0,1] wybieramy dwa losowo dwa punkty (A i B). Jakie jest prawdopodobieństwo, że
| | 1 | |
długość odcinka [A,B] ≤ |
| |
| | 4 | |
| | 1 | | 3 | |
Dla ułatwienia ustalmy, że punkt A ląduje gdzieś pomiędzy ( |
| , |
| ). |
| | 4 | | 4 | |
I masz tutaj wtedy dokładnie taką samą sytuację
15 maj 19:35
Rafal: OK, poczytam trochę i za jakiś czas do tego wrócę.
15 maj 19:37
kochanus_niepospolitus:
oczywiście źle Ci napisałem dając to 'ułatwienie'
bo cały szkopuł polega na tym, co będzie gdy A będzie w przedziale (0 ; 0.25) oraz (0.75, 1) i
tu właśnie będzie to 'uśrednianie' przedziału dla punktu B
15 maj 19:43
Adamm:
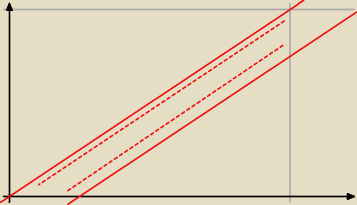
0≤x≤1, 0≤y≤1
szukamy prawd. że |x−y|≤1/4 ⇔ (x−y≤1/4 ∧ x−y≥0) ∨ (x−y≥1/4 ∧ x−y≤0) ⇔
⇔ x−1/4≤y≤x ∨ x≤y≤x−1/4 ⇔ x−1/4≤y≤x
wystarczy obliczyć pole
prawd. wynosi 7/32
15 maj 19:45
Adamm: pomyliłem się w nierówności

bardziej 7/16
15 maj 19:47
kochanus_niepospolitus:
| | 1 | | 1 | | 1 | | 3 | | 7 | |
P(A) = |
| * |
| + |
| * |
| = |
| |
| | 2 | | 2 | | 2 | | 8 | | 16 | |
zapomniałeś o tym, że 'B' może być "nad" A w tym przypadku

15 maj 19:49
Adamm: wyprzedzam przyszłość

15 maj 19:51
Adamm: właśnie, to z okręgiem też można byłoby tak policzyć
| | ∫02πr∫02πr∫0min(|x−y|, 2πr−|x−y|)dzdydx | |
P= |
| |
| | 8π3r3 | |
tylko z tą całką byłby problem, pewnie trzeba byłoby ją rozdzielić na kilka mniejszych
15 maj 19:56
powrócony z otchłani: Da sie ale trzeba by bylo troche sie z tym pobawic z przeksztalceniem okregu na prosta i
wyznaczyc warunki 'odleglosci' C od B i A (ktory domyslnie bylby poczatkiem odcinka)
15 maj 20:04
jc: Stawiam na 5/8.
15 maj 20:31
Adamm: jc, z okręgiem czy to przykładowe zadanie wstawione przez kochanusa?
15 maj 20:33
jc: Z okręgiem, 13:06.
15 maj 20:37
Adamm:
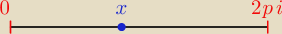
| | ∫0π∫0xdydx+∫π2π∫02π−xdydx | | 1 | |
P= |
| = |
| |
| | 4π2 | | 4 | |
tak będzie moim zdaniem
15 maj 20:43
Adamm: nie podobało mi się uśrednianie w rozwiązaniu kochanusa
15 maj 20:46
jc: Cóż, masz rację, 1/4.
15 maj 20:55
jc:
0 < α < π < b < 2π, β − α < π lub odwrotnie.
15 maj 21:00
 Jeśli chodzi o okrąg to sprawa prosta:
wybieramy kolejno wierzchołka A, B, C
A −−− dowolnie
B −−− dowolnie
C −−− na fioletowej części okręgu (uzależniona jest od pozycji B względem A i środka okręgu)
Jeśli chodzi o okrąg to sprawa prosta:
wybieramy kolejno wierzchołka A, B, C
A −−− dowolnie
B −−− dowolnie
C −−− na fioletowej części okręgu (uzależniona jest od pozycji B względem A i środka okręgu)

 )
)
 Wersja z okręgiem
Załóżmy że wybieramy punkty po kolei. Funkcja gęstości prawdopodobieństwa kąta między
pierwszym a drugim punktem jest stała i równa f(α) = 1/π. Trójkąt będzie ostrokątny jeśli
trzeci punkt znajdzie się na łuku o rozpiętości kątowej α, czyli z prawdopodobieństwem
warunkowym równym α/2π (warunkiem jest że kąt jest równy α).
Szukane prawdopodobieństwo to prawdopodobieństwo całkowite
Wersja z okręgiem
Załóżmy że wybieramy punkty po kolei. Funkcja gęstości prawdopodobieństwa kąta między
pierwszym a drugim punktem jest stała i równa f(α) = 1/π. Trójkąt będzie ostrokątny jeśli
trzeci punkt znajdzie się na łuku o rozpiętości kątowej α, czyli z prawdopodobieństwem
warunkowym równym α/2π (warunkiem jest że kąt jest równy α).
Szukane prawdopodobieństwo to prawdopodobieństwo całkowite

 Punkt 'A' jest wybierany losowo, ale że mamy okrąg to jakbyśmy nie wybrali punkt A, tak
możemy tak przekręcić kartkę aby znalazł się w 'lewym rogu' (nie czepiać się
Punkt 'A' jest wybierany losowo, ale że mamy okrąg to jakbyśmy nie wybrali punkt A, tak
możemy tak przekręcić kartkę aby znalazł się w 'lewym rogu' (nie czepiać się  ).
Podzielmy teraz okrąg na 4 ćwiartki.
Zauważ, że dla każdego (dowolnie wybranego) punktu B istnieje jego odpowiednik B'.
Suma tych długości tych dwóch łuków niebieskiego i zielonego zawsze będzie równa
połowie obwodu okręgu (πr).
Im bliżej B będzie 'dolnej części okręgu' tym mniejszy będzie ten łuk (i dążył do
).
Podzielmy teraz okrąg na 4 ćwiartki.
Zauważ, że dla każdego (dowolnie wybranego) punktu B istnieje jego odpowiednik B'.
Suma tych długości tych dwóch łuków niebieskiego i zielonego zawsze będzie równa
połowie obwodu okręgu (πr).
Im bliżej B będzie 'dolnej części okręgu' tym mniejszy będzie ten łuk (i dążył do
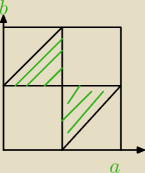
 0≤x≤1, 0≤y≤1
szukamy prawd. że |x−y|≤1/4 ⇔ (x−y≤1/4 ∧ x−y≥0) ∨ (x−y≥1/4 ∧ x−y≤0) ⇔
⇔ x−1/4≤y≤x ∨ x≤y≤x−1/4 ⇔ x−1/4≤y≤x
wystarczy obliczyć pole
prawd. wynosi 7/32
0≤x≤1, 0≤y≤1
szukamy prawd. że |x−y|≤1/4 ⇔ (x−y≤1/4 ∧ x−y≥0) ∨ (x−y≥1/4 ∧ x−y≤0) ⇔
⇔ x−1/4≤y≤x ∨ x≤y≤x−1/4 ⇔ x−1/4≤y≤x
wystarczy obliczyć pole
prawd. wynosi 7/32
 bardziej 7/16
bardziej 7/16


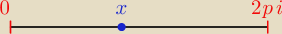
 0 < α < π < b < 2π, β − α < π lub odwrotnie.
0 < α < π < b < 2π, β − α < π lub odwrotnie.