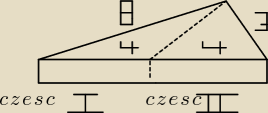
 Serek ma kształt gransiastosłupa, ktorego podstawa jest trojkąt o długosciach bokow ; 8 cm, 8
cm, 3 cm. Konrad i Ola postanowili podzielic serek na dwie części o równych objętościach.
Wojtek lubi skótke pokrywająca całą powierzchnię serka, wieć zaporponował cięcie tak jak na
rysunku. Czy rzeczywiście obie cześci maja tę samą objętość. Ktora częsc ma większa
powierzchnię ze skórka? Odpowiedź uzasadnij.
Serek ma kształt gransiastosłupa, ktorego podstawa jest trojkąt o długosciach bokow ; 8 cm, 8
cm, 3 cm. Konrad i Ola postanowili podzielic serek na dwie części o równych objętościach.
Wojtek lubi skótke pokrywająca całą powierzchnię serka, wieć zaporponował cięcie tak jak na
rysunku. Czy rzeczywiście obie cześci maja tę samą objętość. Ktora częsc ma większa
powierzchnię ze skórka? Odpowiedź uzasadnij.
 ]]
]]











 ? proszeee
? proszeee

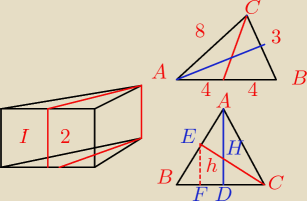 podstawa jest Δ równoramiennym
wykonałam ci trochę rysunków pomocniczych żeby wszysto było lepiej widoczne
Żeby obliczyć V poszczególnych części to musisz znać pole podstawy i wysokość całości
V=PpH1
podstawa jest Δ równoramiennym
wykonałam ci trochę rysunków pomocniczych żeby wszysto było lepiej widoczne
Żeby obliczyć V poszczególnych części to musisz znać pole podstawy i wysokość całości
V=PpH1
| V1 | Pp1 | ||
= | |||
| V2 | Pp2 |
| √55 | ||
H= | ||
| 2 |
| √55 | ||
h= | ||
| 4 |
| 3√55 | ||
P1= | ||
| 8 |
| 3√55 | ||
Pc=12a*H= | ||
| 4 |
| 3√55 | ||
P2= | ||
| 8 |
| Pp1 | |
=1 czyli faktycznie są te kawałki równe
| |
| Pp2 |
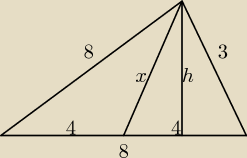 1) Odp. Obie części mają tę samą objętość, gdyż w obu podstawach graniastosłupów jest taka
sama podstawa (4) i równa wysokość podstawy (h).
2) Aby porównać ilość skórki, wystarczy porównać powierzchnie boczne (bo podstawy mają równe
pola).
Pb1 = 4H + xH + 8H
Pb2 = 4H + xH + 3H
8H > 3H ⇒ Pb1 > Pb2
Czyli więcej skórki będzie miała lewa część serka ( o krawędzi 8).
1) Odp. Obie części mają tę samą objętość, gdyż w obu podstawach graniastosłupów jest taka
sama podstawa (4) i równa wysokość podstawy (h).
2) Aby porównać ilość skórki, wystarczy porównać powierzchnie boczne (bo podstawy mają równe
pola).
Pb1 = 4H + xH + 8H
Pb2 = 4H + xH + 3H
8H > 3H ⇒ Pb1 > Pb2
Czyli więcej skórki będzie miała lewa część serka ( o krawędzi 8).

