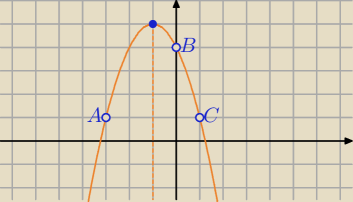
cześc mam zadanie wyznacz rówanie paraboli przechodzącej przez punkty A B C anoio: cześc mam zadanie wyznacz rówanie paraboli przechodzącej przez punkty A B C A(−3,1) B(0,4) C(1,1) czy istnieje możliwość nie rozwiązywania tego układem równań? narazie zrobiłam p=−2+1/2=−1/2 y=a(x+1/2)²+q … w dalszych przekształceniach wyszło mi q=−1/4a+4 znów podstawiłam niestety wychodzi mi 4=1/4a−1/4a+4 proszę o pomoc

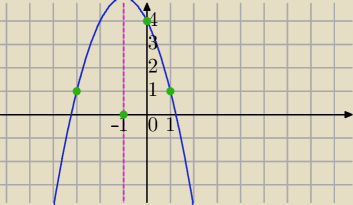
Mila: y=ax²+bx+c B=(0,4) ∊wykresu funkcji⇔c=4 y=ax²+bx+4 f(−3)=f(1)=1⇔

	−3+1
x=		=−1 oś symetrii paraboli,
	2

⇔x_w=−1 to się teraz nie przyda, trzeba układ ( prosty przecież) 1=9a−3b+4 1=a+b+4 a=−1, b=−2 y=−x²−2x+4

Bogdan: Proponuję takie rozwiązanie:

	−3 + 1
oś symetrii x =		= −1, xw = −1
	2

postać kanoniczna f(x) = a(x + 1)² + y_w ⇒ f(x) = ax² + 2ax + a + y_w, a + y_w = 4 f(1) = 1 ⇒ 1 = a + 2a + 4 ⇒ a = −1, −1 + y_w = 4 ⇒ y_w = 5 f(x) = −(x + 1)² + 5 ⇒ f(x) = −x² − 2x + 4

AiO: Istnieje taka mozliwosc Mozna to zrobic wzorem interpolacyjnym Lagrange'a

	(x−x2)(x−x3)
y= y1*		+y2*U{(x−x1)(x−x3)}{(x2−x1)
	(x1−x2)(x1−x3)

	(x−x1)(x−x2)
(x2−x3)}+y3*
	(x3−x1)(x3−x2)

Bogdan: A po co strzelać z armaty do muchy

AiO: To tylko byla odpowiedz na pytanie

Bogdan: To jest banalne zadanie z materiału szkoły średniej na poziomie podstawowym, wzory Lagrange'a na tym poziomie nie są stosowane i taka odpowiedź na tym etapie edukacji nie będzie zrozumiana, myślę, że pamiętasz to z czasu bycia uczniem liceum lub technikum

AiO: Tak

Bogdan: