romb marcinek: Oblicz długość boku rombu ABCD oraz jego pole wiedząc że długości promieni okręgów opisanych na trójkątach ABD i ABC są odpowiednio równe 3 i 4

Mila:

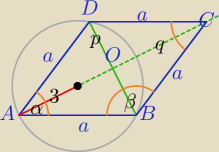
	β		α
β=180−α,		=90−
	2		2

1) W ΔABD: z tw. sinusów:

p		a
	=6=
sinα		sin(90−α2)

	α
p=6*sinα, a=6*cos
	2

2) W ΔABC:

q
	=2*4
sin(180−α)

q
	=8
sinα

q=8sinα 3) W ΔAOB:

	1		1
(		p)2+(		q)2=a2 ⇔(3sinα)2+(4sinα)2=a2
	2		2

	α
9sin2α+16sin2α=(6cos		)2 ⇔25sin2α=36 cos2(α/2)
	2

	α		α		α
25*(2sin		*cos		)2=36 cos2
	2		2		2

	α
100sin2		=36
	2

	α		36		9
sin2		=		=
	2		100		25

	α		4
cos		=
	2		5

4)

	4		24
a=6*		⇔a=
	5		5

============= 5)

	α		α		3		4		24
2*sin		*cos		=2*		*		=		=sinα
	2		2		5		5		25

	24		24
P▱=(		)2*		=..
	5		25

=================

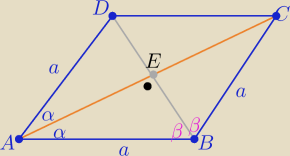Eta: r=3 −− dł promienia okręgu opisanego na ΔABD R=4 −− dł. promienia okręgu opisanego na ΔABC sinβ=cosα Z tw. sinusów w trójkątach ABD i ABC

	a		a		a		a
sinβ=cosα=		=		i sinα=		=
	2r		6		2R		8

	a2		a2
cos2α=		i sin2α=
	36		64

	a2		a2		36*64		48
to		+		=1 ⇒ a2=		⇒ a=
	36		64		100		10

	a		a
P=a2*sin2α= a2*2*		*		= ............
	6		8