Wyznacz zbiór wartości funkcji. 00000:

	3
Wyznacz zbiór wartości funkcji f(x)=		, x∊R, jak zrobić taki przykład? Niby wiem jak
	x2+1

to się robi, ale tylko wtedy jak jest wyznaczony konkretny przedział i nie ma kwadratu w mianowniku. Czy tu trzeba wyznaczyć jakoś wierzchołek paraboli? Z góry dziękuję za pomoc.

Adamm: możesz np. podstawić u=x²≥0 i policzyć zbiór wartości funkcji

	3
g(u)=		dla u≥0
	u+1

albo możesz zrobić tak x²≥0 x²+1≥1

	1
1≥		>0
	x2+1

	3
3≥		>0
	x2+1

i mamy f∊(0;3> albo możesz zrobić

3
	=y
x2+1

0=yx²+y−3 i rozwiązywać jak równanie z parametrem względem y

00000:

	1
dlaczego z x2+1≥1 zrobiło się 1≥		>0 ?
	x2+1

00000: ktoś coś?

Adamm: czemu się uczepiłeś na ten sposób? jak nie wiesz to masz tam podane 2 inne

00000: Problem w tym, Adammie, że sposób ten jedynym jest, który choć trochę rozumiem

Adamm: ok, a co z pierwszym? pierwszy jest bardzo prosty, co w nim nie rozumiesz?

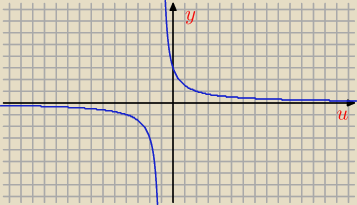
Adamm: wystarczy skorzystać z naszej wiedzy o funkcjach homograficznych, zbiór można odczytać z wykresu z wykresu widać że y∊(0;3>

00000:

	3
Nie umiem policzyć zbioru wartości dla		jak nie mam dokładnie podanych przedziałów,
	u+1

jakby było, nie wiem, np. <1,2>, to robię tak, że 1≤u≤2, a potem dodaję stronami 1 itd, a jak mam tylko podane, że R, to ja nie wiem

00000: Bardzo Ci dziękuję, ale niestety, powiem tak−niestety wiedza o funkcjach homograficznych, nie jest ''nasza'', bo ja pierwszy raz słyszę o czymś takim

Adamm: yhm chyba najlepszy będzie jednak trzeci sposób

3
	=y
x2+1

jeśli dla danego parametru y, równanie ma rozwiązanie, to znaczy że y należy do zbioru wartości funkcji (pomyśl nad tym) można to przekształcić 0=yx²+y−3 jeśli y=0 to 0=−3 czyli y≠0 dla y≠0 liczymy deltę Δ=−4*(y−3)*y i żeby równanie miało rozwiązania Δ≥0 z czego wychodzi nam y∊<0;3>, ale pamiętając o dziedzinie mamy y∊(0;3> czy to do ciebie dociera? chyba ten sposób będzie najlepszy, więc jeśli potrzebujesz dalszych wyjaśnień, mów

00000: Nie umiem liczyć delty, nie było tego jeszcze u mnie w szkole. Mam jeszcze pytanko co do tego drugiego sposobu, skąd się wzięła to 3 linijka i dlaczego jest tam na początku ten przedział, tak jakby (0,1>? Ps. proszę się nie załamywać moją ułomnością.

Adamm: nic nie szkodzi trzeba to tylko zmodyfikować

3−y
	=x2 (założyliśmy że y≠0)
y

3−y
	≥0 (patrz zbiór wartości funkcji x2)
y

(3−y)y≥0 kiedy iloczyn dwóch liczb jest dodatni? kiedy są tego samego znaku (3−y>0 ∧ y>0) ∨ (3−y<0 ∧ y<0) ∨ y=0 ∨ 3−y=0 skąd y∊<0;3>, ale biorąc dziedzinę, y∊(0;3>

Adamm:

3−y
	≥0 mnożysz przez y2 by otrzymać (3−y)y≥0
y

00000: Bardzo Ci dziękuję, spróbuję to jakoś ogarnąć.

Krzysiek:

	3
f(x)=
	x2+1

x=tgy

3		3
	=		=3cos2y
tg2y+1		1   cos2y

3≥3cos²y≥0

Adamm: Krzysiek, dobry sposób ale dla autora bezużyteczny