nierówność trygonometryczna ersia:

	πx
rozwiąż nierówność 2cos		<√2 wyszło mi x∊<4k−1,4k−1/2) ∪ (4k+1/2,4k+3> ... w książce
	2

jest podany wynik (1/2+4k,7/2+4k)czy mógłby mi ktoś powiedzieć czy te wyniki to nie jest to samo?

'Leszek: Podstaw : α = πx/2 i rozwiaz nierownosc cos α < √2/2 , Czyli α ⊂ ( − π/4 + 2kπ ; π/4 + 2kπ ) ⇔ x ⊂ ( −1/2 + 4k ; 1/2 + 4k )

ersia: Leszek dziękuję za odpowiedź ,, Podstaw : α = πx/2 i rozwiaz nierownosc cos α < √2/2'' −właśnie do tego momentu tak zrobiłam i przy rozwiązywaniu tej nierówności wyszedł mi taki wynik : x∊<4k−1,4k−1/2) ∪ (4k+1/2,4k+3> ...zależy mi żeby ktoś odpowiedział czy ten mój to nie jest to samo co napisał Leszek i co jest w książce będe bardzo wdzięczna

ersia: pomoże ktoś?

Mila: Za pół godziny narysuję.

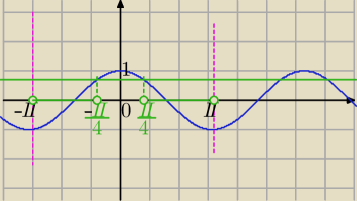
Mila: 1)

	πx		π		π		πx
−π+2kπ<		<−		+2kπ lub		+2kπ<		<π+2kπ /:π
	2		4		4		2

	x		1		1		x
−1+2k<		<−		+2k lub		+2k<		<1+2k /*2
	2		4		4		2

	1		1
−2+4k<x<−		+4k lub		+4k<x<2+4k
	2		2

lub 2)

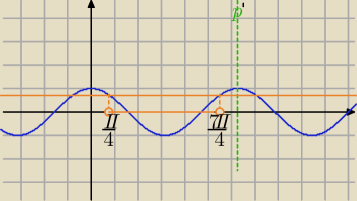
Mila: 2)

π		πx		7π
	+2kπ<		<		+2kπ /:π
4		2		4

1		x		7
	+2k<		<		+2k⇔
4		2		4

1		7
	+4k<x<		+4k
2		2

ersia: Mila bardzo dziękuję za odpowiedź ..jeszcze jedno pytanie a czy mogę zapisać :

−π

πx

−π

π

πx

3π

+2kπ≤

<

+2kπ lub

+2kπ<

≤

+ 2kπ ... Twoje

2

2

4

4

2

2

rozwiązanie rozumiem ale nie wiem czy taka opcja jak napisałam też jest poprawna..bardzo proszę o wyjaśnienie

Mila: Nie jest dobra , ponieważ pomijasz część rozwiązań. Długość przedziału w którym szukasz rozwiązań powinna być równa 2π. i tak: 20:27 masz rozw. w przedziale (−π, π) 20:32 masz rozw. w przedziale (0,2π)

ersia:

	−π		3π
hmm a ja szukałam rozwiązań w przedziale (		,		} ...ten przedział też ma długość
	2		2

2π ... przepraszam że się tak dopytuję ale zależy mi na pełnym zrozumieniu błędu w mojej odpowiedzi

Mila:

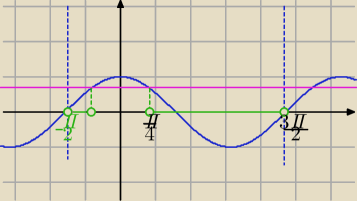
π

πx

π

π

πx

3π

−

+2kπ<

<−

+2kπ lub

+2kπ<

<

+2kπ /:π

2

2

4

4

2

2

	1		x		1		1		x		3
−		+2k<		<−		+2k lub		+2k<		<		+2k
	2		2		4		4		2		2

	1		1
−1+4k<x<−		+4k lub		+4k<x<3+4k
	2		2

Masz dobrze, nie skojarzyłam wcześniej w jakim przedziale to rozpatrywałaś.

ersia: okej , to już wszystko rozumiem ogromnie dziękuję Mila <3

Mila: